Реферат: Широкополосное согласование комплексных нагрузок на основе теории связанных контуров
![]() (6)
(6)
Из (5) и (6) с учетом (4) определим обобщенный фактор связи ![]() , соответствующий заданному качеству согласования
, соответствующий заданному качеству согласования ![]() , то есть заданному значению
, то есть заданному значению ![]()
![]() (7)
(7)
Приравнивая правую часть (7) выражению для ![]() из (2), определим фактор связи
из (2), определим фактор связи ![]() соответствующий заданному
соответствующий заданному ![]()
![]() (8)
(8)
Обобщенную расстройку ![]() , соответствующую краю полосы согласования, определим из условия равенства
, соответствующую краю полосы согласования, определим из условия равенства ![]() единице
единице
![]() (9)
(9)
Отсюда, с учетом (7) и выражения для ![]() из (2), получаем требуемую для обеспечения заданного качества согласования полосовую добротность нагрузочного контура
из (2), получаем требуемую для обеспечения заданного качества согласования полосовую добротность нагрузочного контура
![]() (10)
(10)
Минимально возможная величина ![]() равна полосовой добротности нагрузки
равна полосовой добротности нагрузки ![]() При этом соотношение (10) является предельным для двухзвенной полиномиальной чебышевской СЦ. Из него следует соотношение
При этом соотношение (10) является предельным для двухзвенной полиномиальной чебышевской СЦ. Из него следует соотношение
![]()
связывающее качество согласования с добротностью и полосой согласования нагрузки при согласовании ее двухзвенной полиномиальной чебышевской СЦ.
Если полиномиальная цепь не дает удовлетворительного качества согласования, что может быть при ![]() больше единицы, следует провести оптимизацию СЦ по критерию минимума
больше единицы, следует провести оптимизацию СЦ по критерию минимума ![]() в заданной полосе согласования. Для этого следует предположить, что ни на одной из частот СЦ не обеспечивает идеального согласования. В этом случае
в заданной полосе согласования. Для этого следует предположить, что ни на одной из частот СЦ не обеспечивает идеального согласования. В этом случае
![]() . (11)
. (11)
Из (11), (9) и выражений для ![]() и
и ![]() из (2) следует уравнение, связывающее основные параметры двухзвенной СЦ
из (2) следует уравнение, связывающее основные параметры двухзвенной СЦ
![]() (12)
(12)
Оптимальное значение ![]() , соответствующее максимуму
, соответствующее максимуму ![]() , то есть минимуму
, то есть минимуму ![]() , находится приравниванием производной правой части (12) по
, находится приравниванием производной правой части (12) по ![]() и равно
и равно
![]() (13)
(13)
Соответствующее ![]() минимальное значение
минимальное значение ![]() находится из (12) с учетом (13) и равно
находится из (12) с учетом (13) и равно
![]() . (14)
. (14)
Минимальное значение ![]() в полосе согласования при этом определяется из выражения
в полосе согласования при этом определяется из выражения ![]()
где ![]()
При ![]() соотношение (14) является предельным для двухзвенной оптимизированной чебышевской СЦ. Расчеты показывают, что оптимизированная таким образом СЦ является оптимальной в смысле Боде-Фано.
соотношение (14) является предельным для двухзвенной оптимизированной чебышевской СЦ. Расчеты показывают, что оптимизированная таким образом СЦ является оптимальной в смысле Боде-Фано.
Аналогичным образом полученные предельные соотношения для одно-, двух- и трехзвенных полиномиальных и оптимальных СЦ с максимально плоской и чебышевской характеристиками рабочего затухания сведены в табл. 1.
Таблица 1.
| Тип цепи | Однозвенная СЦ |
| Полиномиальная | |
| Оптимальная | |
| Двухзвенная СЦ |
| Полиномиальная | Чебышевская | |
| Максимально плоская | ||
| Оптимальная | Чебышевская | |
| Максимально плоская | 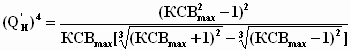 |
| Трехзвенная СЦ |
| Полиномиальная | Чебышевская | 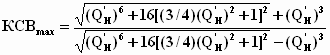 |
| Максимально плоская | ||
| Оптимальная | Чебышевская |
К-во Просмотров: 353
Бесплатно скачать Реферат: Широкополосное согласование комплексных нагрузок на основе теории связанных контуров
|