Реферат: Синтез частотно-избирательного фильтра
5. Определить координаты нулей и полюсов передаточной функции синтезируемого частотно-избирательного фильтра. Построить график АЧХ с использованием денормированной частоты ![]() .
.
6. Определить лестничную структуру синтезируемого фильтра с нормированными элементами и провести денормирование элементов.
7. Выбрать возможные варианты RLC-звеньев первого и второго порядков, предназначенных для каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
8. Уменьшив частотные параметры на два порядка:
8.a. Составить схему и провести расчет элементов для гираторной реализации фильтра.
8.b. Выбрать возможные варианты ARC-звеньев первого и второго порядков, предназначенные для безиндукционной каскадной реализации фильтра, рассчитать величины элементов и составить полную схему фильтра.
9. Сделать вывод, дав сравнительную характеристику различным вариантам реализации синтезируемого фильтра.
Исходные данные
Задача синтеза фильтра состоит в разработке электрической схемы устройства, обладающего требуемыми частотными и временными характеристиками. Курсовая работа предполагает проектирование фильтра на основе требования к форме его характеристики затухания. При синтезе полосно-пропускающего фильтра вводится требование к верхним и нижним граничным частотам полосы пропускания (![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
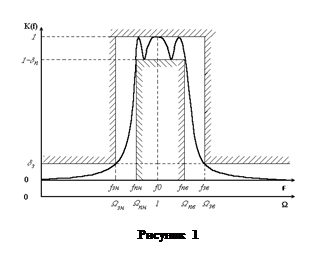 Амплитудно-частотная характеристика (АЧХ) фильтра
Амплитудно-частотная характеристика (АЧХ) фильтра ![]() и характеристика затухания
и характеристика затухания ![]() связаны друг с другом выражением
связаны друг с другом выражением
![]() ,
,
поэтому при рассмотрении требований к АЧХ необходимо вместо допусков ![]() и
и ![]() ввести параметры:
ввести параметры: ![]() - допустимую неравномерность в полосе пропускания и
- допустимую неравномерность в полосе пропускания и ![]() - максимально допустимую передачу в полосе задержания, причем
- максимально допустимую передачу в полосе задержания, причем
![]() ,
, ![]() .
.
Типичная АЧХ полосно-пропускного фильтра Чебышева приведена на рисунке.
Процедура проектирования частотно-избирательного фильтра включает в себя два основных этапа:
1. Этап проектирования , в ходе которого подбирается передаточная функция, удовлетворяющая заданным требованиям (АЧХ, выделенная из аппроксимирующей передаточной функции, не должна выходить за пределы заданного коридора допусков);
2. Этап реализации , суть которого – в выборе принципа реализации передаточной функции, разработке и расчете конкретной схемы фильтра, обладающего найденной передаточной функцией.
Порядок выполнения первого этапа достаточно хорошо разработан, поставленная задача решается с использованием какого-либо из многочисленных справочников по расчету фильтров. Решение второй задачи в рамках второго этапа многовариантно. Это связано с тем, что известно довольно много принципов и схем, позволяющих реализовать найденную передаточную функцию.
Аппроксимация частотной характеристики фильтра
Последовательность шагов
На этапе аппроксимации необходимо проделать следующее:
1. Выбрать тип фильтра.
2. Пересчитать исходные данные в требования к фильтру – прототипу нижних частот (ФНЧ-прототипу).
3. Определить минимальный порядок ФНЧ-прототипа, нули и полюсы его передаточной функции (с помощью справочника).
4. Пересчитать нули и полюса ФНЧ-прототипа в нули и полюсы синтезируемого фильтра.
5. Записать передаточную функцию фильтра, найти и построить АЧХ или характеристику затухания.
Тип фильтра
Существует ряд типов фильтров, различающихся по характеру их передаточных функций. Например, фильтр Баттерворта, фильтр Чебышева, эллиптический (Золоторева - Каура) фильтр. Каждый из указанных типов в определенном смысле оптимален. Главная же особенность состоит в том, что заданную избирательность фильтр Чебышева обеспечивает при меньшем порядке, чем фильтр Баттерворта, а эллиптический фильтр в этом смысле лучше чебышевского.
Требования к ФНЧ-прототипу
Для того чтобы не было привязки начального этапа расчета к конкретным значениям частоты и, следовательно, приводимые в справочниках таблицы и графики имели большую общность, осуществляется нормировка частотной оси и ее трансформация таким образом, чтобы свести характеристики ФНЧ, ФВЧ, ППФ, ПЗФ к характеристикам эквивалентного ФНЧ-прототипа.
Амплитудно-частотная характеристика ФНЧ-прототипа определена на нормированной оси частот, причем граничная частота полосы пропускания ![]() , а граничная частота полосы задержания
, а граничная частота полосы задержания ![]() . В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания
. В качестве нормирующей частоты для ФНЧ и ФВЧ выбирается граничная частота полосы пропускания ![]() , а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания)
, а для ППФ и ПЗФ – центральная частота полоса пропускания (задержания) ![]() . Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой (
. Формулы для вычисления нормированных частот синтезируемого фильтра и его ФНЧ-прототипа приведены в таблице 2.1.[1] Обозначение частоты с тильдой (![]() ) относится к проектируемому фильтру, а без тильды (
) относится к проектируемому фильтру, а без тильды (![]() ) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии
) – к ФНЧ-прототипу. При синтезе ППФ и ПЗФ определяется коэффициент геометрической асимметрии ![]() , в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия:
, в зависимости от значения, которого по-разному вычисляют нормированные частоты. Важно проконтролировать, чтобы всегда выполнялись условия: ![]() и
и ![]() . В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.
. В противном случае невозможно правильное преобразование ППФ и ПЗФ из ФНЧ-прототипа.