Коммуникации и связь / Реферат: Состав элементной базы СМЭ

Реферат: Состав элементной базы СМЭ

Для упрощения проектирования, процессы обработки информационных сообщений и электрических преобразований сигналов чаще всего связывают через третий (буферный) процесс — функциональное преобразование сигналов. Под функциональным преобразованием будем понимать отображение (переход) одного состояния или кодовой комбинации сигналов в другое состояние или кодовую комбинацию.

Информационные сообщения могут быть сформированы с помощью как аналогового, так и дискретного преобразования (кодирования). При дискретном кодировании одно слово сообщения формируется путем составления определенных комбинаций из многих сигналов,

Рис. 2. Классификация функциональных преобразований сигнала.

которые имеют ограниченное число состояний^* , а их параметры изменяются, как правило, скачкообразно. В связи с таким разделением способов формирования сообщений появилось три вида преобразователей: аналоговые, дискретные (цифровые) и смешанные (рис. 2).

При смешанных преобразованиях состояние входных сигналов может изменяться непрерывно (как во времени, так и по уровню), а состояние выходных сигналов — дискретно и наоборот. Возможно совместное преобразование аналоговых и дискретных сигналов. С помощью известной теоремы В.А. Котельникова аналоговые сигналы можно преобразовывать в смешанные или полностью дискретные, почти не искажая их информационного содержания.

Функциональные преобразования могут быть детерминированными или вероятностными. В первом случае каждому состоянию или кодовой комбинации входных сигналов однозначно соответствует только одно состояние или одна кодовая комбинация выходных сигналов из множества возможных. Во втором случае соответствие между состояниями и кодовыми комбинациями входных и выходных сигналов задается вероятностными законами.

Дискретные функциональные преобразования разделяются на два больших класса: импульсные и логические; первые широко применяются в радиосвязи, радиолокации, радионавигации, телевидении и т. п.; вторые используются в устройствах кодирования и декодирования в радиотехнических системах, цифровой телеметрии, вычислительной технике и автоматических устройствах управления. Аргументы логических функций и сами функции принимают только два значения: «нуль».или «единица» (0 или 1). Эти преобразования или, как их еще называют, логические операции подчиняются законам математической логики. В табл. 1 показано различие аналоговых, импульсных и логических преобразований.

Таблица 1

Характеристики преобразования	Виды преобразования
	Аналоговые	импульсные			логические
	Аналоговые	варианты преобразований			логические
Число состояний сигналов по шкале времени	∞	∞	n_t	n_t	2
Число состояний сигналов по шкале уровней	∞	n_y	∞	n_y	2
Число сигналов, формирующих одно слово сообщения	1	p₁	p₂	p₃	l
Число возможных комбинаций сигналов, формирующих одно слово сообщения	—	1	1	1	m

Примечание. Здесь m — число дискретных сигналов (объем алфавита): n_t и n_y — число квантованных изменений параметров сигналов по времени и по уровню.

Для того чтобы как-то систематизировать множество аналоговых, цифровых и смешанных функциональных преобразований, выделим в каждом из них три подкласса: генерирование сигналов, усиление и трансформация сигналов, формирование сигналов.

Первый и второй подклассы пояснений не требуют. В третий подкласс сведены все преобразования, связанные с изменением формы и Спектрального состава сигналов. Это наиболее обширный подкласс, включающий модуляцию и детектирование сигналов, смешение, фильтрацию, ограничение и т. д. Форма и спектральный состав сигналов связаны между собой известными преобразованиями Фурье. Следовательно, можно взять за основу изменение формы сигналов (временной подход) или изменение спектрального состава (спектральный подход). При дальнейшей классификации подкласса формирования сигналов, приведенной на рис. 2, выбран спектральный подход. Используя теоремы о спектрах, можно выделить в этом подклассе, по крайней мере, шесть видов математических преобразований, указанных в табл. 2.

Таблица 2

Название теорем о спектрах	Математическая формулировка теорем	Примеры технического использования
Теорема о спектре производной сигнала		Дифференцирование сигналов
Теорема о спектре интегрирования сигнала		Интегрирование сигналов
Теорема о смещении сигнала по шкале времени		Задержка сигналов
Теорема о сумме спектров		Смещение и фильтрация сигналов
Теорема о спектре произведения (свёртка функций)		Умножение на весовую функцию
Теорема подобия спектров		Временное сжатие сигналов

Каждая микросхема, решающая ту или иную функциональную задачу, состоит из ряда элементарных функциональных преобразователей (ЭФП). Сложность каждого преобразователя зависит от сложности синтезируемой микросхемы, её конкретных свойств и квалификации проектировщика. Конечным продуктов функционального синтеза все чаще становится мелкомасштабная часть микросхемы.

Все ЭФП можно условно разбить на две категории: электрические ЭФП, с помощью которых в процессе функционального синтеза ИС можно моделировать преобразования электрических сигналов, и так называемые специальные ЭФП, отражающие функциональные механизмы преобразования неэлектрических величин в электрические сигналы и дополняющие связь ИС с аппаратурой и внешней средой. Специальные ЭФП можно разбить на четыре класса: механические (ЭФП перемещения, ускорения, веса, объема и т. п.), физические (ЭФП магнитные, оптические, тепловые и т. п.), химические (ЭФП концентрации и т. п.) и биологические (ЭФП биопотенциальные, фоторецепторные, метаболические).

Электрические ЭФП можно разделить на четыре класса: аналоговые (АЭФП), импульсные (ИЭФП), смешанные (СЭФП) и логические (ЛЭФП). Первые два класса в свою очередь разбиваются на подклассы: ЭФП генерирования сигналов, ЭФП усиления и трансформации сигналов и ЭФП формирования сигналов. Последний обширный подкласс ЭФП удобно подразделить еще на две группы: ЭФП индивидуального формирования сигнала (ограничение, умножение и деление частоты, дифференцирование и интегрирование, задержка во времени т. п.) и ЭФП группового формирования сигналов (модуляция и детектирование, смешение и фильтрация, различение сигналов и т. п.). Смешанные ЭФП подразделяются на два подкласса: ЭФП видеосигналов и ЭФП радиосигналов. Логические ЭФП подразделяются на ЛЭФП с запоминанием (управляемые и неуправляемые) и ЛЭФП без запоминания (статические и динамические).

Каждый ЭФП характеризуется своим символом и определяющими его параметрами^* . В качестве символа ЭФП мы выбрали прямоугольник со значком или буквами в середине (отражающими назначение преобразования или форму выходного сигнала) и внешними стрелками, характеризующими число входов и выходов. Параметры ЭФП удобно проставлять по внешнему периметру символа. Число параметров зависит от типа ЭФП и точности преобразования, задаваемой Проектировщиком (мы проставим только наиболее характерные из них). В табл. 3 приводится далеко не полный перечень преобразований, используемых в аналоговых, импульсных, смешанных и логических ЭФП [1.4].

Таблица 3

Принципиальная схема		Тип преобразования
Аналоговые ЭФП
		Генерирование синусоидального сигнала: — частота автоколебаний; — нестабильность частоты; — амплитуда выходного напряжения
		Усиление: — амплитуда входного напряжения (тока); — коэффициент усиления по напряжению (току), — полоса пропускания
		Двустороннее ограничение напряжения (тока): и — соответственно верхний и нижний пороги ограничения; — коэффициент изменения величины сигнала после ограничения
		Умножение частоты: — амплитуда входного сигнала; — частота входного сигнала; — коэффициент умножения частоты; — коэффициент изменения амплитуды (мощности) сигнала
Принципиальная схема	Тип преобразования
	Деление частоты: — амплитуда входного сигнала; — частота входного сигнала; — коэффициент деления частоты
	Фильтрация: — верхняя частота среза; — нижняя частота среза; — коэффициент прямоугольности на уровне ; — коэффициент передачи
	Смешение: — амплитуда первого входного сигнала; — амплитуда второго входного сигнала; и — частоты первого и второго сигналов; — коэффициент пропорциональности между входными сигналами
	Амплитудная модуляция: — амплитуда несущего сигнала; — амплитуда модулирующего сигнала; — коэффициент, характеризующий глубину модуляции; — частота несущего сигнала; — частота модулирующего сигнала
Импульсные ЭФП
	Генерирование прямоугольных импульсов: — длительность импульса; — величина импульсного напряжения (тока); — частота повторения импульсов; — длительность переднего фронта импульса
	Генерирование линейно изменяющего (пилообразного) сигнала: — время прямого (обратного) хода сигнала; — максимальная величина сигнала; и — коэффициенты нестабильности амплитуды и скорости нарастания сигнала; — коэффициент нелинейности прямого хода сигнала
	Дифференцирование прямоугольного импульса: — напряжение (ток) входного импульса; — длительность выходных импульсов (на уровне 0.5); — коэффициент передачи
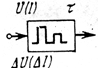	Интегрирование прямоугольного импульса: — напряжение (ток) входного импульса; — длительность выходного импульса (на уровне 0.5)
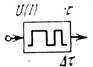	Разделение импульсов по амплитуде: — напряжение (ток) выделяемых импульсов; — допустимый разброс селекции
	Разделение импульсов по длительности: — длительность выделяемых импульсов; — допустимый разброс
Смешанные ЭФП
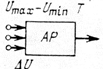	Различение амплитуды (): — диапазон изменения величины аналогового сигнала; — допустимый разброс чувствительности амплитудного различения
	Амплитудное детектирование радиоимпульсов: — амплитуда несущего сигнала; — частота несущего сигнала; — длительность радиоимпульсов; — величина выходного сигнала после детектирования
Логические ЭФП
	Сложение сигналов (дизъюнкция). Символически записывается или (сигнал на выходе существует, если на входы подан хотя бы один сигнал)
	Умножение сигналов (конъюнкция). Символически записывается (сигнал на выходе существует, если на все входы поданы сигналы)
	Отрицание сигнала (инверсия). Символически записывается ;

Число типов аналоговых, импульсных и смешанных ЭФП весьма велико. В отличие от указанных типов ЭФП полная система переключательных ЛЭФП (функции с двумя состояниями) разработана еще Дж. Булем в прошлом веке. Таких ЛЭПФ всего 16. Помимо приведенных и табл. 3, существуют еще ЛЭФП эквивалентности или равнозначности , импликации в , Шеффера , Вебба , сложения по модулю 2 и другие. Принцип действия перечисленных ЛЭФП показан в табл. 4.