Реферат: Судоку и хроматические многочлены

Мы кратко рассмотрим вопрос единственности решения для задачи Sudoku. В начале не всегда ясно имеет ли данная задача решение. В этой части, мы получим необходимые условия для того, чтобы быть определить единственное решение.

На рисунке 1. пример задачи судоку, которая имеет точно два решения.

Это наблюдение лидирует в следующее замечания. Если в решении в задачу судоку мы указали бы, что конфигурация на рисунке 3 в том же вертикальном стеке, тогда по крайней мере одно из этих данных должны быть включены как "данный" в начальной задаче, в противном случае, у нас было бы два возможных решения в начальной задаче возникающие просто перестановкой a и b в конфигурации.

Как замечено ранее, если точное число "цветов" использованных в данной задаче судоку - самое большее семь, тогда есть по крайней мере два решения в задачу. Мы отметим, что это было таким поскольку мы могли взаимообмен два неиспользованных цвета и все еще получать правильное решение. Множественность решений может также видна из хроматического многочлена. Если d0 количество использовавшихся цветов, мы видели, что pX3,C (m), полином по m, m> d0. Так как хроматическое число X3 = 9, мы должны иметь pX 3 C (m) = 0 для m = d0,d0 + 1,...,8. Как pX 3C (m), полином с целыми коэффициентами, мы можем записать pX3,C (m) = (m - d0) (m- (d0+ 1)) … (m-8) q (m), для некоторого полинома q (ь) с целыми коэффициентами. При m = 9 получаем pX3,C (9) = (9-d0) Б=q (9) и право сторонняя сторона больше или равна 2 если d0>= 7. Это дает нам установленное необходимое условие для там, чтобы было единственное решение, при условии, что у задачи есть решение.

Заключение

Интересно отметить, что задача судоку чрезвычайно популярна по нескольким причинам. Заслуживает внимания то, что эта задача судоку вызвала несколько проблем математической природы, которые пока нерешены. Мы уже упомянули проблему "минимальной задачи судоку", где мы спрашиваем, если есть задача судоку с 16 или меньшими данными, которые допускают единственное решение.

Мы уже прокомментировали что, если только 7 или меньшее количество цветов использованы, задача не имеет единственного решения.

Эти вопросы предполагают более общий вопрос определения "минимума судоку" для общей задачи ранга n.

Мы уже отмечали различные симметрии квадратов судоку. Например, применяя перестановку к элементам {1,2,..., n2}, мы получим новый квадрат судоку. Таким образом, начиная с одного такого квадрата, мы можем произвести n² ! новых судоку. Есть также ленточные перестановки их n!, а также перестановки столбцов, которых также n!. Мы можем переставить колонки в пределах полосы, а также столбцы в пределах стека - n! ⁿ симметрий. В итоге, это генерирует группу симметрии, которые могут быть рассмотрены как подгруппа Sn4. Будет интересным определить размер и структуру этой подгруппы.

Список использованных источников

1. S. Bammel and J. Rothstein, The number of 9 × 9 Latin squares, Discrete Math.11 (1975), 93-95.

2. C. D. Godsil and B. D. McKay, Asymptotic enumeration of Latin rectangles, J.comb. Theory Ser. B 48 (1990), no.1, 19-44.

3. B. Felgenhauer and A. F. Jarvis, Mathematics of Sudoku I, Mathematical Spectrum 39 (2006), 15-22.

4. E.russell and A. F. Jarvis, Mathematics of Sudoku II, Mathematical Spectrum 39 (2006), 54-58.

5. J. H. Van Lint and R. M. Wilson, A Course in Combinatorics, Cambridge University Press, 1992.

Приложение

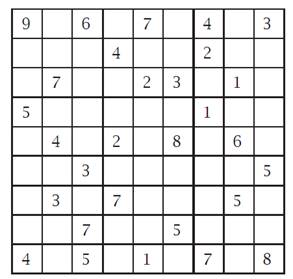
Рис. 1

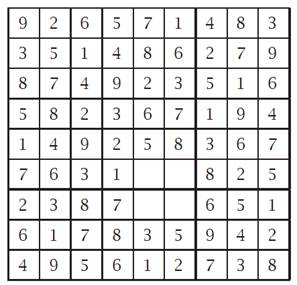
Рис. 2

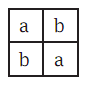
Рис. 3