Реферат: Трионы: три тела в двух измерениях

f(x)≈2.718 - 8.155x+12.232x² +...,

до тех пор пока не угадать, что второе есть всего лишь разложение первого в степенной ряд.

Для построения такой вариационной функции необходимо правильно учесть все эффекты, которые вносят основной вклад в энергию системы. В том, как и в какой форме их учесть, есть определенный элемент творческого "угадывания". Как правило, функции, построенные таким образом, труднее интегрировать, чем набор простых функций, который использовался в первом подходе, поэтому использовать их для высокоточных вычислений путем увеличения подгоночных параметров обычно нецелесообразно. Зато даже при использовании небольшого количества параметров они дают значение энергии системы с хорошей точностью. Пойдем по второму пути и посмотрим, как построить хорошую функцию с небольшим, числом подгоночных параметров, которая позволила бы получить энергию основного состояния триона при любом значении отношения масс электрона и дырки. Необычность задачи состоит в том, что одна и та же функция при различных значениях вариационных параметров должна с хорошей точностью описывать не только Х+ и X" трионы, но и предельные случаи - ион водорода Н" и молекулу водорода Н2+, различие между волновыми || функциями которых очень велико. В качестве основы для нашей функции возьмем двумерный аналог пробной функции, предложенной в 1944 году Чандрасекаром [10] для трехмерного иона водорода H^- :

ψ(r₁ ,r₂ )=[ехр(-ar₁ -br₂ )+ехр(-br₁ -ar₂ )](1+cR), (1)

Она состоит из симметризованного произведения двух водородоподобных функций с различными радиусами орбит электронов и поляризационного множителя. Величины r₁ и r₂ r₁ -r₂ |. Вариационные параметры а и b имеют смысл обратных радиусов орбит двух электронов, а параметр c обеспечивает рост волновой функции при увеличении расстояния между электронами, то есть учитывает поляризационные эффекты.

Функция (1) учитывает, пусть и в простом виде, все эффекты, которые вносят основной вклад в энергию иона. А именно:

1. Кулоновское взаимодействие каждого из электронов с ядром.

Функция (1) содержит в основе водородоподобные функции (exp(-ar)).

2. Экранирование дальнего электрона ближним.

В слагаемое ехр(-ar₁ -br₂ ) волновые функции электронов (ехр(-ar₁ ,ехр(-br₂ )) входят с разными показателями экспонент, что соответствует различным радиусам орбит электронов.

3. Обменное взаимодействие.

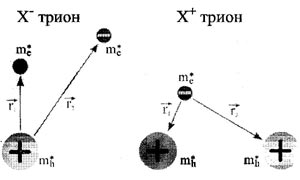Рис 1. X- и X+ трионы, общий вид

Волновая функция симметризована и не меняется при замене r₁ ↔r₂ , то есть допускает обмен электронов.

4. Поляризация.

Как уже упоминалось, она учтена наличием множителя (1+сR).

Так как эти вклады присутствуют и являются основными как для трехмерного иона H^- , так и для его двумерного аналога, то неудивительно, что с помощью функции (1) получается хорошее приближение энергии связи иона. В обоих случаях ошибка в определении энергии составляет менее 10% от ее значения (за нуль энергии принято состояние атом водорода + свободный электрон).

Посмотрим, что изменится, если мы применим волновую функцию (1) к трионам с различными значениями отношения масс. Заметим, что волновая функция триона должна содержать в своей основе функцию основного состояния экситона (электрон + дырка), которая совпадает по форме ехр(-аr) с функцией атома водорода. Причем, энергия триона (в особенности - X^- триона) должна определяться вкладами тех же, как и в ионе H^- , эффектов: поляризации, экранирования и обменного взаимодействия. Поэтому есть основания предполагать, что с помощью функции (1) можно с неплохой точностью (не худшей, чем для иона водорода) получить энергию любого X^- триона.

Проблема возникает при моделировании X⁺ трионов по мере приближения к противоположному от H^- пределу - молекуле H₂ ⁺ , в связи с наличием у них двух тяжелых частиц. В этом пределе движение этих частиц "замораживается", и они перестают вносить вклад в кинетическую энергию комплекса. Это приводит к известному факту, что энергия связи молекулы H₂ ⁺ почти в 4 раза превышает энергию связи иона H^- . При увеличении отношения масс электрона и дырки вблизи предела H₂ ⁺ , кинетическая энергия колебаний двух тяжелых частиц, возрастающая пропорционально корню из этого отношения масс, очень быстро начинает вносить существенный вклад в энергию, триона. Уже при отношении масс σ=0.1 энергия связи этого комплекса уменьшается почти вдвое по сравнению с пределом H₂ ⁺ (σ→0). Поэтому для правильного вычисления энергии X⁺ триона, особенно при малых отношениях масс, необходимо в дополнение к вышеперечисленным эффектам учесть возможность продольных колебаний одинаковых частиц возле некоторого равновесного расстояния. Так как других эффектов, которые могут внести большой вклад в энергию триона при каком-либо отношении масс больше не видно, то пробная функция, в которой все эти эффекты будут учтены, должна с хорошей точностью давать энергию комплекса при любом отношении масс.

Пример такой функции приведён в работе [11]:

ψ(r₁ ,r₂ )=[ехр(-ar₁ -br₂ )+ехр(-br₁ -ar₂ )](1+cR)exp(-sR)/(1+d(R-R₀ )² ), (2)

где, в дополнение к определенным выше величинам a, b и с, введены подгоночные параметры d и R₀ , которые учитывают возможные малые колебания с характерной амплитудой 1/√d возле равновесного расстояния

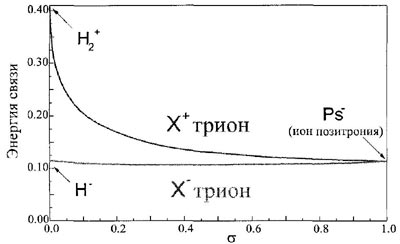Рис 2. Энергия связи X+ (красный) и X- (синий) трионов в зависимости от отношения эффективных, масс электрона и дырки. Энергия нормирована на энергию связи экситона

R₀ и параметр s для оптимизации функции триона при больших расстояниях между одинаковыми частицами.

Выбор множителя функции (2), 1+d(R-R₀ )² , отвечающего за продольные колебания комплекса, несложно обосновать. Заметим, что в случае, если связь между двумя одинаковыми частицами триона можно описать параболическим потенциалом, то волновая функция (2) должна зависеть от R (расстояния между этими двумя частицами) по Гауссу:

ψ(R)~ехр(-d(R-R₀ )² ).

Но это приближение справедливо лишь для очень малых колебаний дырок комплекса X⁺ и только в пределе молекулы H₂ ⁺ (при очень малых σ). Реально потенциал, связывающий две одинаковые частицы в трионе, на больших расстояниях гораздо слабее параболического, и гауссовское приближение волновой функции триона приведет к гораздо более быстрому ее убыванию с расстоянием, чем это есть в действительности. Поэтому выбрана более слабая зависимость:

ψ(R)~1/(1+d(R-R₀ )² ),

которая неплохо даёт первое приближение колебаний триона вблизи R=R₀ , а поведение функции ψ(R) на бесконечности было задано более слабым, чем гауссовская функция, множителем exp(-sR).

Зависимость энергии связи триона от отношения масс, полученная с помощью функции (2), приведена на рис.2. Несмотря на простоту подгоночной волновой функции, мы получили эту зависимость с хорошей точностью: энергия связи триона при любом отношении масс составляет более 95% от ее точного значения, которое известно из более серьезных расчетов [7,9] с использованием большого числа вариационных параметров.

Обратим также внимание на то, что энергия связи триона (нормированная на энергию связи экситона) практически одинакова для X^- (≈0.12) и не зависит от отношения масс электрона и дырки; в то время как для X⁺ она растет по мере приближения к H₂ ⁺ , причем основной рост приходится на область σ < 0.1. На этом участке энергия связи триона возрастает с 0.22 (при σ = 0.1) до 0.41 (при σ = 0) - почти в два раза. А при σ = 0 производная энергии по отношению масс даже имеет корневую особенность. Это, как уже упоминалось, связано с исчезновением колебательной степени, свободы в X⁺ трионах при малых отношениях масс [11].

4. Заключение

Мы показали, что, для того, чтобы найти энергию X^- и X⁺ трионов при любом отношении масс с хорошей точностью, достаточно учесть вклад пяти факторов: кулоновского притяжения двух электронов к дырке (будем говорить в терминах X^- ), экранирования дальнего электрона ближним, обменного взаимодействия между электронами, поляризации экситона дальним электроном и продольных колебаний двух электронов друг относительно друга. Как оказалось, несложная вариационная функция, построенная из таких соображений, позволяет вычислить энергию связи X^- и X⁺ трионов с хорошей точностью во всем диапазоне отношений масс электрона и дырки.

[1]* Имеется в виду размерность k-пространства, то есть число независимых направлений, в которых движение частицы с данной энергией не квантовано.

Список литературы