Реферат: Углеродные нанотрубки

Контуром в графе называется замкнутая цепочка ребер, объединение которых представляет собой линию, гомеоморфную окружности.

Деревом называется связный граф, не содержащий ни одного контура.

Индекс точки называется число дуг, сходящихся в данной точке.

Также следует доказать следующую теорему:

Для любого дерева, имеющего В вершин и Р ребер, справедливо соотношение

В-Р=1. (2)

Для доказательства проведем индукцию по числу ребер Р. При Р=1 (дерево имеет одно ребро и две вершины) соотношение (2) справедливо. Предположим, что для любого дерева, имеющего n ребер, соотношение (2) уже доказано, и пусть G - дерево, имеющее n+1 ребро. Так как граф G связен, то его можно получить из некоторого связного графа G` добавлением одного ребра r.

Действительно, любой связный граф может быть получен следующим образом: мы берем одно ребро, затем присоединяем к нему еще одно ребро так, чтобы снова получился связный граф, затем присоединяем еще одно ребро (так, чтобы снова получился связный граф) и т.д. Это возможно, если удастся его вычертить «одним росчерком». А это, в свою очередь, возможно, если разрешить «проходить» каждое ребро ровно два раза.

* * *

Докажем, что любой связный граф можно вычертить «одним росчерком», если разрешить проходить каждое ребро точно два раза.

Если проходить граф описанным выше способом, то его можно сопоставить с графом, у которого приходится по два ребра на каждое ребро исходного графа, т.е. индекс каждой вершины в два раза больше, чем у исходного. Полученный граф имеет вершины с четными индексами, а значит этот граф является уникурсальным (его можно «нарисовать одним росчерком»).

* * *

Граф G` содержит n ребер и тоже не содержит контуров, т.е. является деревом. По предположению индукции для дерева G` соотношение (2) справедливо, и потому в G` имеется n+1 вершина. Заметим теперь, что только один конец добавляемого ребра r является вершиной графа G` (в противном случае, взяв в G` простую цепочку, соединяющую a и b, и добавив к этой цепочке ребро r, мы получили бы контур в графе G). Следовательно, при добавлении ребра r в графе G появляется одно новое ребро и одна новая вершина. Иначе говоря, граф G имеет n+2 вершины и n+1 ребро, и потому соотношение (2) для него справедливо. Проведенная индукция доказывает равенство (2) для любого дерева.

Теперь можно приступить к доказательству теоремы Эйлера. Для ее доказательства выделим из графа G максимальное его дерево G^* , обозначим за k - число «перемычек» (т.е. ребер графа G, не содержащихся в G^* ). Т.к. граф G^* является деревом, то он не содержит ни одного контура, а, следовательно, он определяет на сфере лишь одну область (грань), и потому для него соотношение (1) справедливо. Далее, добавляя одну «перемычку», число ребер увеличивается на единицу, число вершин остается прежним, т.к. G^* - максимальное дерево, т.е. оно содержит все вершины графа G; число граней увеличится на единицу за счет разбиения одной грани на две. Отсюда видно, что добавление одной «перемычки» не меняет соотношения (1). Значит и добавление k перемычек его не изменит. Т.е. граф G удовлетворяет соотношению (1).

Из теоремы Эйлера можно получить несколько интересных следствий.

Обозначим через n₃ число треугольных граней выпуклого многогранника, через n₄ - число его четырехугольных граней и т.д. Тогда соотношение один можно переписать так:

В=2+Р-(n₃ +n₄ +n₅ +...). (3)

Т.к. каждое из ребер «принадлежит» ровно двум граням, то можно записать следующую формулу:

Р= (4)

В каждой вершине же сходится минимум три грани, т.е. каждой грани «принадлежит» максимум вершин, отсюда вытекает неравенство:

(5)

Объединяя (3), (4) и (5), получим

Умножая полученное на 6 и приводя подобные, получим:

причем равенство возможно только в том случае, когда в вершине сходятся три грани. В нашем случае, для идеальных фулеренов и для нанотрубок, запаянных с обоих концов это выполнено. Отсюда видно, что в состав них может входить ровно 12 пятиугольников.

Вторым следствием теоремы Эйлера является так называемая эйлерова характеристика поверхности.

Пусть Q — поверхность, которая допус­кает разбиение на многоугольники; это означает, что на поверхности можно «нарисовать» граф, разбивающий ее на конечное число кусков, гомеоморфных кругу. Обозначим число вершин и ребер графа через В и Р, а число многоугольников, на которые Q разбивается этим графом,— через Г. Число

X (Q) = В - Р + Г (6)

называется эйлеровой характеристикой поверхности Q. Строго говоря, число (6) определяется не самой поверхностью Q, а выбором ее разбиения на многоугольники. Однако теорема Эйлера показывает, что для поверхности Q, гомеоморфной сфере, эйлерова характеристика не зависит от выбора разбиения на многоугольники: Х(Q)=2. Докажем, что и для любой поверхности Q ее эйлерова характеристика Х(Q) не зависит от выбора разбиения на многоугольники, а определяется самой по­верхностью.

В самом деле, пусть на, поверхности Q «нарисованы» два графа G₁ , G₂ , каждый из которых задает разбиение на многоугольники. Числа вершин, ребер и граней разбиения, определяемого графом G₁ , обозначим через B₁ , Р₁ , Г₁ , а соответствующие числа для разбиения, определяемого графом G₂ ,— через В₂ , Р₂ , Г₂ . Вообще говоря, графы G₁ и G₂ могут пересекаться в бесконечном числе точек. Однако, «пошевелив» граф G₁ , мы сможем добить­ся того, чтобы G₁ и G₂ пересекались лишь в конечном числе точек.

Далее, если граф G₁ G₂ несвязен, то, «пошевелив» графы G₁ , G₂ , можно добиться того, чтобы они имели общие точки и, следовательно, их объединение было связным. Итак, мы можем предполагать, что графы G₁ и G₂ пересекаются лишь в конечном числе точек и имеют связ­ное объединение G₁ G₂ . Считая новыми вершинами все точки пересечения графов G₁ и G₂ , а также все вершины этих графов, мы найдем, что G₁ G₂ является конечным связным графом (его ребрами являются куски ребер графов G₁ и G₂ , на которые они разбиваются вершинами графа G₁ G₂ ).

Обозначим через В и Р число вершин и ребер графа G₁ G₂ , a через Г — число граней, на которые он разбивает поверхность Q. Идея состоит в том, чтобы доказать равенства

(7)

из которых и будет следовать, что B₁ -P₁ +Г₁ =B₂ -P₂ +Г₂ . Оба равенства (7) доказываются одинаково; докажем первое.

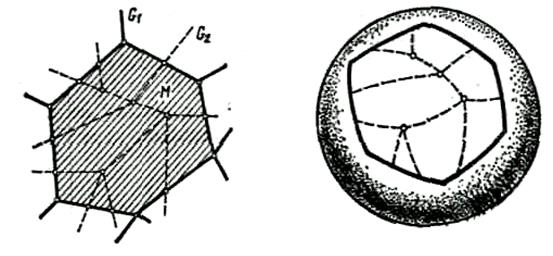
Пусть М - некоторый многоугольник («грань»), определяемый графом G₁ . Обозначим число вершин и ребер графа G₁ G₂ , расположенных внутри М (не на контуре), через В' и Р', а число вершин (а значит, и ребер) этого графа, расположенных на контуре многоугольника М, через q. Далее, число граней, определяемых графом G₁ G₂ и содержащихся в М, обозначим через Г'. На рис. 4 имеем В'=4, Р'=12, Г'=9, q=15.

Вырежем теперь многоугольник М (вместе с имеющейся на нем частью графа G₁ G₂ ) из поверхности Q. Так как М гомеоморфен кругу и, значит, полусфере, то его можно второй («нижней») полусферой дополнить до поверхности, гомеоморфной сфере (рис. 5). На этой сфере расположен связный граф, имеющий В'+q вершин, Р'+q ребер и определяющий Г'+1 граней (Г' граней содержится в М и еще одной гранью является нижняя полусфера). Следовательно, согласно (1), (В'+q)- (Р'+q)+(Г'+1)=2, т. е.

В'-Р'+Г=1. (8)

Если теперь (возвращаясь к поверхности Q, на которой начерчен граф G₁ G₂ ) мы выбросим из графа G₁ G его часть, расположенную внутри М, то получится новый граф, для которого, однако, число В-Р+Г останется таким же, как и для графа G₁ G₂ . В самом деле, вместо В' вершин, Р' ребер и Г' граней, имевшихся внутри М, мы теперь будем иметь 0 вершин, 0 ребер и одну грань (сам многоугольник М), т. е. число В'-Р'+Г' заменится на 0-0+1, а это, согласно (8), ничего не меняет.