Реферат: Универсальная геометрия в природе и архитектуре
Понятие симметрии, развиваемое Пьером Кюри, шире обыденного понимания симметрии как, например, зеркальное равновесие масс, и предполагает, прежде всего, симметрию как движение, как развитие, как отношение отрицания единичных свойств тела и среды и утверждения их общих свойств в форме особенного, порожденного ими нового тела (2,10,18). Другим примером динамической симметрии является процесс метаболизма, свойственный органическим формам, как единство синтеза и распада. При очевидном различии (жизнь и смерть), эти процессы находятся в отношении симметрии.
В научной методологии, смысл симметрии (отношений) так же предполагает, что фундаментальный закон должен быть инвариантным по отношению к действию некоторой операции симметрии (преобразования координат, функциональные преобразования и т.п.).
3. СИММЕТРИЯ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
3.1. Геометрия специальной теории относительности . Соответствует ли принципам симметрии модель пространства-времени, разработанная специальной теорией относительности с целью органичного включения открытой физической постоянной – скорости света в физическую теорию, взамен представлениям Ньютона, об отсутствии ограничений на скорость?
Геометрическим способом введения в физику световой константы и светоподобного интервала является псевдоевклидова геометрия (теорема Пифагора, связывающая в псевдоевклидовой метрике абсолютный и относительные интервалы пространства и времени). Пространство-время представлено ортогональными координатами и разделено образующими, для которых x = t (это взаимно-перпендикулярные, развернутые вокруг центра системы отсчета (x,t) под углом ![]() образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1 ). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени:
образующие (ct,-ct). Они разделяют ИСО на две области: область до световых скоростей и область сверхсветовых скоростей. Область до световых скоростей, в свою очередь, состоит из области прошлого и области будущего (Рис.1 ). Квадрат абсолютного интервала равен разности квадратов относительных интервалов пространства и времени:![]() ,
,![]() .
.
3.2. Нарушение принципа симметрии специальной теорией относительности . Отметим следующие нарушения принципа симметрии в модели ИСО СТО:
1. Кроме скорости v (абсолютной скорости пробной частицы), и скорости с (абсолютной скорости света), в уравнениях присутствует скорость![]() , физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения)
, физический смысл которой не ясен, кроме того, что она входит в выражение коэффициента Лоренцева сокращения (расширения)![]() . Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.
. Как производная абсолютных скоростей v и c, она должна иметь аналогичный смысл и указывает на существование некоторого реального физического объекта, с движением которого она связана.
2. При ![]() равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/
равноправной v и c, отношения c/c = 1/1 = 1 и c/v = 1/![]() так же должны иметь смысл адекватный смыслу
так же должны иметь смысл адекватный смыслу![]() . Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО , со своими коэффициентами сокращения (расширения).
. Иначе, предположительно, в световой модели Вселенной должны существовать три типа равноправных ИСО , со своими коэффициентами сокращения (расширения).
3. Введение понятия светоподобного интервала, в связи с открытием в природе предельной скорости света (граничные параметры скоростей v=0, v=c), предполагает два типа равноправных ИСО, для которых состояние покоя формулируется относительно граничных параметров скорости света:![]() , состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и
, состояние покоя которой соответствует скорости v=0 (система отсчета Лоренца-Минковского в СТО) и![]() , состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную
, состояние покоя которой соответствует скорости света (фотон, как покоящаяся система). СТО не рассматривает такую равноправную![]() . При заданном условии покоя v=c),
. При заданном условии покоя v=c), ![]() покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основанияхкак
покоится на образующих светоподобного конуса (сt ,-ct) на таких же законных основанияхкак ![]() покоится при v=0.
покоится при v=0. ![]() зеркальна
зеркальна![]() . Если
. Если ![]() расширяется, то
расширяется, то![]() – сокращается. Скорость частицы в
– сокращается. Скорость частицы в ![]() -
-![]() ,
, ![]() = c/v=
= c/v=![]() . Так как - v в
. Так как - v в ![]() и
и ![]() в
в ![]() связаны скоростью света (или светоподобным интервалом),
связаны скоростью света (или светоподобным интервалом), ![]() и
и ![]() являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения -
являются относительными, связанными между собой светоподобным интервалом, подсистемами одной и той же системы отсчета. Иначе, светоподобный интервал это не только предельная величина скорости, что утверждает СТО, но, прежде всего, скорость, связывающая две равноправные, но качественно различные ИСО покоя в движении одной и той же “пробной массы”, т.е. системы отсчета присущих ей различных форм движения, например, как частицы - v и как излучения -![]() . Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и
. Эти скорости могут быть связаны с различной плотностью массы пробной частицы (например, v – скорость положительной плотности +p и ![]() - скорость отрицательной плотности -p ).
- скорость отрицательной плотности -p ).
4. В связи с тем, что в ИСО Минковского часть пространства-времени связана с досветовыми скоростями (конуса будущего и прошлого), а часть - со сверхсветовыми скоростями, она не только полностью не определена, но допускает нарушение исходного принципа своей конструкции – движение со сверхсветовой скоростью. Если допустить существование сверхсветовых скоростей, мы, при конструировании ИСО, должны отказаться от скорости света, связанного с ней ![]() и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.
и определяться в новом геометрическом принципе ИСО. Но это уже будет совершенно другая система отсчета.
5. В уравнении закона сохранения (например, для абсолютного интервала массы покоя![]() ):
):
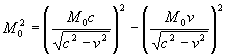 1)
1)
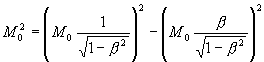
![]() 2)
2)
Где ![]() - абсолютный интервал t-подобной массы покоя
- абсолютный интервал t-подобной массы покоя
![]() - относительный интервал t-подобной энергии;
- относительный интервал t-подобной энергии;
![]() - относительный интервал x-подобного импульса
- относительный интервал x-подобного импульса
об абсолютной природе интервала ![]() можно говорить лишь в относительном смысле, в связи с применением
можно говорить лишь в относительном смысле, в связи с применением![]() , так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме
, так как по аналогии с правой частью равенств 1) и 2), абсолютный интервал в левой части равенства, может быть выражен в форме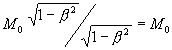 . Интервал абсолютен только при
. Интервал абсолютен только при![]() .
.
Поскольку 1/1, 1/![]() не могут рассматриваться иначе, как равноправные
не могут рассматриваться иначе, как равноправные ![]() (наравне с
(наравне с![]() ), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно
), ясно, что масса покоя 1),2) теряет свой абсолютный смысл, если ее рассматривать относительно ![]() = 1/
= 1/![]() или
или ![]() = 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при
= 1/1, т.е. представление абсолютности интервала 2) справедливо лишь при![]() .
.
3.3. Незавершенность геометрии ИСО в СТО. Внутренние (нарушение симметрии в уравнении скоростей, наличие несистемных областей пространства-времени) и внешние (независимость системы отсчета от материи, неточность отражения движения в связи с гравитационными эффектами) противоречия ИСО в СТО, необоснованность выражения пространственно-временного континуума теоремой Пифагора в связи с принципиально различной природой пространства (как протяженной характеристики) и времени (как длительной характеристики), позволяют сделать вывод, что ограниченность ИСО в СТО связана, прежде всего, с незавершенностью, неразвернутостью геометрии ее координатного пространства.
4. ПРЕОБРАЗОВАНИЕ СИСТЕМЫ ОТСЧЕТА МИНКОВСКОГО
С учетом вышесказанного, преобразование ИСО СТО Минковского, с целью снятия противоречий, предполагает две главных процедуры (рис.1, рис.2):
4.1. Мнимый поворот координатных осей пространства-времени Минковского .
А) Мнимый поворот х-подобной оси х (ИСО СТО) на ![]() до совмещения с отрицательной полуосью времени -t (конус прошлого) и превращением ее в отрицательную мнимую величину -iх , противонаправленную времени t (Г.Корн, Т.Корн. Справочник по математике, -М.: Наука, 1973, с.31-33). Закон сохранения (для интервала массы покоя) приобретает следующее выражение:
до совмещения с отрицательной полуосью времени -t (конус прошлого) и превращением ее в отрицательную мнимую величину -iх , противонаправленную времени t (Г.Корн, Т.Корн. Справочник по математике, -М.: Наука, 1973, с.31-33). Закон сохранения (для интервала массы покоя) приобретает следующее выражение:
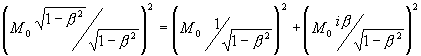 3)
3)
Поворот не изменил отношений в формуле 2). Пространственный вектор ![]() приобрел отрицательный знак относительно положительного вектора и заменил суммой разность между двумя квадратами относительных интервалов ИСО СТО, но при этом, вошедшая в выражение импульса мнимая единица, вернула нас вновь к разности квадратов интервалов.
приобрел отрицательный знак относительно положительного вектора и заменил суммой разность между двумя квадратами относительных интервалов ИСО СТО, но при этом, вошедшая в выражение импульса мнимая единица, вернула нас вновь к разности квадратов интервалов.
Б) Этому повороту соответствует аналогичный поворот и совмещение -ct и ct (далее![]() ) и, кроме того, общий поворот совмещенных осей (
) и, кроме того, общий поворот совмещенных осей (![]() ) на
) на ![]() в положение, перпендикулярное совмещенным осям (T,iХ ), т.е в положение, занимаемое осью пространства ИСО СТО :
в положение, перпендикулярное совмещенным осям (T,iХ ), т.е в положение, занимаемое осью пространства ИСО СТО :
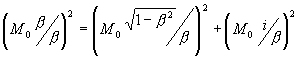 4)
4)
![]()
Относительный интервал энергии (![]()
![]()
![]()
![]() ) получил зеркальную, x -подобную форму, относительный интервал импульса (Мо* 1/
) получил зеркальную, x -подобную форму, относительный интервал импульса (Мо* 1/![]() ), наоборот, t-подобную форму, абсолютный интервал Мо*
), наоборот, t-подобную форму, абсолютный интервал Мо* ![]() /
/![]() – x-подобную форму. Взятые относительно светоподобного интервала
– x-подобную форму. Взятые относительно светоподобного интервала ![]() = 1/1, уравнения приобретают абсолютно идентичную количественную форму с зеркальной метрикой: свойство абсолютного интервала приобретает энергия (x -подобная и t- подобная), абсолютные интервалы в уравнениях 3) и 4) приобретают роль относительных импульсов. Абсолютные, комплексные: t-подобный
= 1/1, уравнения приобретают абсолютно идентичную количественную форму с зеркальной метрикой: свойство абсолютного интервала приобретает энергия (x -подобная и t- подобная), абсолютные интервалы в уравнениях 3) и 4) приобретают роль относительных импульсов. Абсолютные, комплексные: t-подобный ![]() и x-подобный
и x-подобный ![]() интервалы энергии связывают в псевдоевклидовой геометрии Минковского пары относительных осевых противоположно направленных импульсов, при этом :
интервалы энергии связывают в псевдоевклидовой геометрии Минковского пары относительных осевых противоположно направленных импульсов, при этом :