Реферат: Уроки в інтегральній технології навчання за В. Гузеєвим

Класифікацію методів навчання можна побудувати по-різному в залежності тому, яке відношення покласти в основу.

Як основне відношення використовуватимемо відвертість елементів цієї схеми для учня. Якщо учень знає, з якого знання треба виходити, через які проміжні результати пройти у вивченні теми, яким чином їх досягти, то його функції в навчанні зводяться до того, щоб запам'ятати і в потрібний момент відтворити все це. Таким чином, можна говорити про репродуктивний або пояснювально-ілюстративний метод навчання. Якщо до учня не доводяться проміжні результати, але відкрито все інше, то маємо програмоване навчання. Дійсно, учень знає, з чого виходити і що робити. Отримавши результати по першій частині програми дій, треба перейти до виконання другої частини програми, і так далі до отримання планованих результатів.

Процес в цьому випадку повністю детермінований.

Хай тепер відкриті проміжні результати, але про спосіб їх отримання учням не повідомляється. Тоді доводиться пробувати різні шляхи, користуючись безліччю евристик, і так повторюється після кожного оголошеного проміжного результату (мал.2а – наведено нижче).

Перед нами стандартна схема евристичного пошуку, тобто ми говоримо про евристичний метод навчання. Тепер можна заховати і проміжні результати, і шляхи їх досягнення. Тоді учень має суперечність між наявними і необхідними знаннями і потрапляє в проблемну ситуацію. Його пошук набуває складнішого характеру (мал. 26). У такому разі вчителем вибраний проблемний метод навчання.

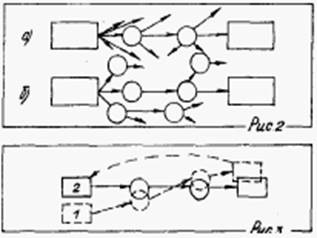
Розглянуті методи будувалися на тому, що учень знав початкові умови. Це досягалося домашнім завданням, ввідним повторенням, спеціальними формами опиту і так далі. Проте останнім часом все більшою популярністю користується навчання, коли початкові умови вчителем не виділяються, а відбираються самим учнем залежно від його розуміння задачі. З цих умов він одержує результати, порівнює їх з планованими, а при отриманні розбіжностей з метою повертається до початку, вносить зміни в свої початкові умови і знов проходить весь шлях (мал. 3).

Весь цей процес повторює процес моделювання, унаслідок чого і метод отримав назву модельного. Не виключено, що закриваючи від учня різні елементи схеми разом з початковими умовами, ми отримаємо різновиди модельного методу, наприклад, модельно-евристичний.

Матриця різноманітності форм

Отже, ми можемо отримати таблицю класифікації методів навчання:

Застосовувати кожний метод навчання можна в різних організаційних формах. Якщо відомі форми організації уроку виписати по термінах прямокутної таблиці, а по стовпцях розташувати п'ять методів навчання, ми отримаємо так звану матрицю різноманітності форм.

Вчитель, охочий оцінити свою різноманітність, може, не одурюючи себе, поставити хрестики в тих клітках, які, на його думку, відповідають методам і формам, ним освоєним, знаходяться в його активному арсеналі. Наприклад, якщо вчитель уміє проводити класичний семінар, то може відзначити відповідну клітку (Семінар, ОИ), оскільки класичний семінар проводиться пояснювально-ілюстративним методом. Якщо ж він упевнено проводить на уроках ділові ігри (наприклад, його коник – урок-пресс-конференція), то відзначитиклітку (Семінар, М), оскільки ділова гра – це не що інше, як модельний метод. Розставивши таким чином хрестики, вчитель побачить, над чим йому можна і потрібно тепер попрацювати, а це дозволить скласти індивідуальну програму самоосвіти, здійснювати цілеспрямований пошук професіонально значущої інформації.

Клітина в матриці відзначена, якщо її вказали більше п'ятдесяти відсотків опитаних. Оскільки в класифікації методів немає одноманітності, то в подібних обстеженнях треба робити зусилля по уніфікації мови. У зв'язку з цим нелишне помітити, що в кожній з шкіл дослідження проводилося відразу після того, як автор цієї статті прочитав на педраді лекцію "Системний підхід до педагогічної технології", унаслідок чого термінологія була прийнята вчителями і вони могли порівняти свої уявлення з продемонстрованими прикладами з різних наочних областей. Нижче показаний типовий набір з арсеналумасового вчителя:

Форма/Метод	ОИ	ПГ	Е	ПБ	М
Розповідь	Х	Х
Бесіда	Х	Х
Лекція	Х
Семінар	Х
Семінар-Практикум
Практикум
Практична робота	Х
Лабораторна робота	Х	Х
Екскурсія	Х	Х	Х
Консультація
Самостійні роботи	Х	Х	Х

Аналогічно може поступити адміністрація будь-якої школи. Для цього треба розмножити матрицю по числу вчителів, видати кожному (наприклад, на педраді), і після заповнення зібрати. Потім всі отримані дані можна звести в одну матрицю. На мал. 7 приведена зведена матриця однієї з обстежених шкіл (32 вчителі).

Форма/Метод	ОИ	ПГ	Е	ПБ	М
Розповідь	32	17
Бесіда	32	32
Лекція	32	3
Семінар	28	1
Семінар-Практикум	1
Практикум	7	4
Практична робота	26	3
Лабораторна робота	20	17	2	1
Екскурсія	30	17	19
Консультація	2
Самостійні роботи	32	29	17	18	1

Можна в цих клітках писати як абсолютна кількість виборів, так і в процентному відношенні до числа вчителів. Тут під кількістю виборів ми розумітимемо кількість вчителів, що відзначили дану клітку. В приведеній матриці вказані абсолютні числа виборів. Зведена матриця може виявитися більш наочною, якщо кожний вибір відзначати крапкою.

Отримавши цей масив інформації зворотного зв'язку, можна тепер управляти самоосвітою вчителів. Зведена матриця дозволяє планувати методичну роботу школи в цілому. Для нашого прикладу це могло б виглядати так. Судячи з результатів, практично ніхто в колективі не володіє проблемним і модельним методами. Значить, за наявності засобів можна замовити лекції фахівцям, а при їх відсутності, доручити деяким вчителям вивчити літературу, а потім передати придбані знання іншим через шкільний методичний семінар або методичне об’єднання.

Потім можна домовитися, хто проведе відкриті уроки для загального обговорення, і так далі. З цієї ж матриці можна зробити висновок, що вчителі даної школи не знають такої форми уроку, як семінар-практикум. Ця форма – елемент інтегральної технології навчання. Далі, судячи з матриці, вчителі не володіють методикою організації і проведення консультацій.

Тепер, спланувавши тривалу методичну роботу школи в цілому, можна дати індивідуальні рекомендації вчителям по їх самоосвіті. Для цього достатньо в матриці, заповненій кожним вчителем, виділити вільні клітки, не перекриті загальним планом. В результаті вийде не тільки особистий план самоосвіти, але і в деякому роді прогноз розвитку професійних якостей вчителя. Можливість такого прогнозу цінна для адміністрації будь-якої школи.

Пропонований інструмент придатний для демократичного рівня управління, коли самоосвіта вчителів йде в співпраці з діяльністю адміністрації. Хотілося б застерегти від завзятого адміністрування, бажання використовувати даний механізм як засобу контролю і оцінки професійної якості вчителів. В цьому сумному випадку матриця різноманітності форм може стати двосічною зброєю і привести до непотрібних конфліктів.

Наступний етап в управлінні самоосвітою може бути пов'язаний з оволодінням цілими моделями навчання і конкретними педагогічними технологіями, адаптацією їх до своїх умов. Це відкриває шлях до побудови авторських концепцій навчання.

Список використаної літератури:

1. Ангеловські К.;«Учителя и инновации»; М., 1991 р.;

2. Гребенюк О.С. Педагогика индивидуальности. - Калининград, 1995.

3. Гузеев В.В. Лекции по педагогической технологии. - М., 1992.

4. Казанский Н.Г., Назарова Т.С.; «Дидактика (начальные классы)» М., 1978 р.

5. Кларін М.В. Инновационные модели обучения в зарубежных педагогических поисках. - М., 1994.

6. Коляшин Ю.М., Луканкін Г.Л., Саннінський В.Л.; «Методика викладання математики в середній школі»;М., 1980 р.;

7. Паламарчук В., Рудаківська С.; «Від творчої особистості – до нових технологій у навчанні»//Рідна школа, 1998 р. - №2.3;

8. Махмутов М.И., Ибрагимов Г.И. Педагогические технологии развития мышления. - Казань, 1993.

9. Монахов В.М. Проектирование и внедрение новых технологий обучения // Советская педагогика. - 1990. - №7.