Реферат: Усталостная прочность материалов

Диаграмма предельных напряжений (диаграмма Смита) строится, как минимум, по трем режимам нагружения (по трем точкам), для каждого из которых определяют предел выносливости.

Первый режим (точка 1) – обычный симметричный цикл нагружения (, , , ).

Второй режим (точка 2) – асимметричный цикл нагружения, как правило, отнулевой (, , , ).

Третий режим (точка 3) – простое статическое растяжение (, ).

Полученные точки соединяют плавной линией, ординаты точек которой соответствуют пределам выносливости материала при различных значениях коэффициента асимметрии цикла.

Луч, проходящий под углом через начало координат диаграммы предельных напряжений, характеризует циклы с одинаковым коэффициентом асимметрии R :

.

Диаграмма предельных амплитуд (диаграмма Хейга) строится в координатах: среднее напряжение цикла – амплитуда цикла (рисунок 7). При этом для ее построения необходимо провести усталостные испытания так же как минимум для трех режимов: 1 – симметричный цикл; 2 – отнулевой цикл; 3 – статическое растяжение.

Соединяя полученные точки плавной кривой, получают график, характеризующий зависимость между значениями предельных амплитуд и значениями предельных средних напряжений в цикле.

Кроме свойств материала, на усталостную прочность оказывают влияние следующие факторы: 1) наличие концентраторов напряжений; 2) масштабный фактор, то есть влияние абсолютных размеров детали (чем больше размеры детали, тем ниже усталостная прочность); 3) качество обработки поверхности (с уменьшением шероховатости поверхности детали растет усталостная прочность); 4) эксплуатационные факторы (температура, коррозия, частота нагружения, радиационное облучение и т.д.); 5) наличие поверхностного слоя, упрочненного различными технологическими методами.

напряжение усталость кривая прочность

3. Расчет на прочность при циклических напряжениях

Расчет на прочность при циклических напряжениях начинают с построения диаграммы усталостной прочности (часто, для простоты рассуждений предельную линию представляют в виде прямой) и показывают на ней рабочую точку М цикла в случае, если рассматриваемый элемент испытывает только простое растяжение и сжатие.

Рассмотрим все те циклы, рабочие точки которых лежат на одной прямой, и для которых справедливо выражение s_à =s_m ∙tga. Тогда .

Значит, можно сделать вывод о том, что все подобные циклы лежат на одной прямой. Тогда, под запасом усталостной прочности будем понимать отношение отрезка ON к отрезку OM : , где точка M соответствует действующему циклу, а точка N получается вследствие пересечения предельной прямой и продолжения отрезка OM .

Для определения (т.е. в ситуации, когда действуют лишь нормальные напряжения) в инженерной практике применяются как графический, так и аналитический способы. При графическом способе строго по масштабу строится диаграмма предельных напряжений в системе координат. Далее, на этой диаграмме наносится рабочая точка и определяется отношение величин отрезков ON и OM . Для определения расчетных зависимостей для воспользуемся условием подобия треугольников OND и OMK и получим:

.

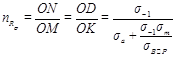Полученный коэффициент запаса соответствует идеальному образцу. Реальная же его величина зависит, как отмечалось выше, от геометрии, размеров и состояния поверхности образца, учитываемых коэффициентами К _1 , соответственно. Для этого необходимо предел усталости при симметричном нагружении уменьшить в раз, или, что тоже самое, амплитудное напряжение цикла увеличить в раз. Тогда

,

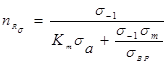где .

Аналогичным образом могут быть получены соотношения усталостной прочности и при чистом сдвиге. Эксперименты показывают, что диаграмма усталостной прочности для сдвига заметно отличается от прямой линии, свойственной простому растяжению (сжатию), и имеет вид кривой. В первом приближении эту кривую в координатных осях _a , _m можно представить в виде двух наклонных, как это изображено на рисунке 9. Причем, если одна из них (ближняя к оси ординат) соответствует разрушению образца вследствие усталостных явлений, то другая  по причине наступления пластического состояния.

В данном случае расчетная формула для записывается в виде

,

где  эмпирическая величина, определенная на основе обработки экспериментальных данных.

При сложном напряженном состоянии, т.е. если в рабочей точке при действии внешних нагрузок одновременно возникают как нормальные, так и касательные напряжения, для вычисления n_R применяется следующая приближенная формула:

,

где n_R искомый коэффициент запаса усталостной прочности;

коэффициент запаса усталостной прочности в предположении, что касательные напряжения в рабочей точке отсутствуют;

 коэффициент запаса прочности по усталости при предположении, что в рабочей точке нормальные напряжения отсутствуют.