Реферат: Вимушені механічні й електромагнітні коливання
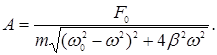 (6)
(6)
Початкова фаза вимушених коливань, як видно з векторної діаграми, дорівнює
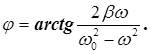 (7)
(7)
З урахуванням співвідношень (6) і (7) розв’язок диференціального рівняння вимушених коливань (2) матиме вигляд
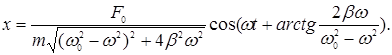 (8)
(8)
Якщо розглянути електричний коливальний контур, то роль змінної величини в цьому випадку буде мати е.р.с., або змінна напруга
![]() (9)
(9)
Диференціальне рівняння вимушених коливань в коливальному контурі, з урахуванням (9), буде мати вигляд
![]() (10)
(10)
Використовуючи позначення, аналогічні до (2), прийдемо до рівняння
![]() (11)
(11)
Розв’язком рівняння (11) є функція, аналогічна до (3), тобто
![]() (12)
(12)
Амплітуда заряду вимушених електромагнітних коливань буде дорівнювати
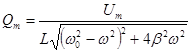 . (13)
. (13)
Підстановка значень ![]() і
і ![]() в (13) дає значення амплітуди електромагнітних коливань в такому вигляді
в (13) дає значення амплітуди електромагнітних коливань в такому вигляді
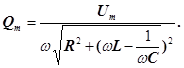 (14)
(14)
Похідна за часом від (12) дає можливість одержати в коливальному контурі закон зміни електричного струму
![]() ,
,
де ![]() ─ максимальний струм у коливальному контурі.
─ максимальний струм у коливальному контурі.
2. Амплітуда і фаза вимушених коливань (механічних і електромагнітних). Резонанс. Резонансні криві. Парамет-ричний резонанс
Розглянемо залежність амплітуди А вимушених механічних або електромагнітних коливань від частоти ω. Механічні й електромагнітні коливання будемо розглядати одночасно, називаючи коливну величину або зміщенням (х) коливного тіла від положення рівноваги, або зарядом (Q ) конденсатора.
З формули (3.6) випливає, що амплітуда А зміщення має максимум. Щоб визначити резонансну частоту ![]() — частоту, при якій амплітуда А зміщення досягає максимуму, — потрібно дослідити на максимум функцію
— частоту, при якій амплітуда А зміщення досягає максимуму, — потрібно дослідити на максимум функцію ![]() . Диференціюємо підкореневий вираз цієї функції по ω і прирівнюємо його до нуля:
. Диференціюємо підкореневий вираз цієї функції по ω і прирівнюємо його до нуля:
![]() ,
,
![]()
Ця рівність виконується при двох умовах ![]() і
і ![]() фізичний зміст яких має лише позитивне значення. Отже, резонансна частота буде дорівнювати
фізичний зміст яких має лише позитивне значення. Отже, резонансна частота буде дорівнювати
![]() (15)
(15)
Явище різкого зростання амплітуди вимушених коливань при наближенні частоти вимушеної сили до ![]() , називається резонансом (відповідно механічним або електричним). У випадку коли
, називається резонансом (відповідно механічним або електричним). У випадку коли![]() значення
значення ![]() практично збігається з власною частотою
практично збігається з власною частотою ![]() коливної системи. Підставляючи (15) у формулу (6), одержимо
коливної системи. Підставляючи (15) у формулу (6), одержимо