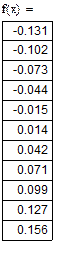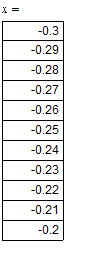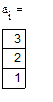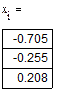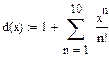Реферат: Вычисление корней нелинейного уравнения

При а =0.1

Интервал изменения параметра x

Строим график функции

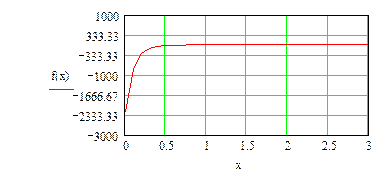
При интервале изменения коэффициента x

График имеет вид

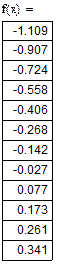
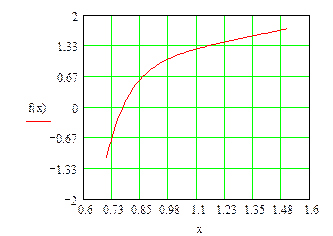
При а=0 функция f(x)=0 имеет значения корня x=0.77

Находим более точное значение корня

-вычислительный блок

-процедура нахождения корня

-более точное значение корня

Проверка:

При а =1

Интервал изменения параметра x

Строим график функции

При интервале изменения коэффициента x

График имеет вид

При а=1 функция f(x)=0 имеет приближенное значения корня x=0,21

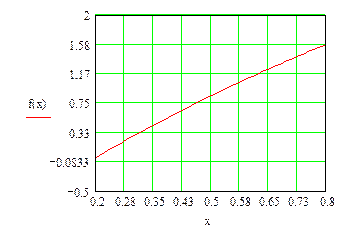
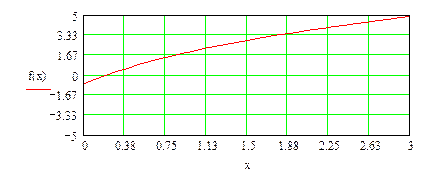
Находим более точное значение корня

-вычислительный блок

-процедура нахождения корня

-более точное значение корня

Проверка:

При а =2

Интервал изменения параметра x

Строим график функции

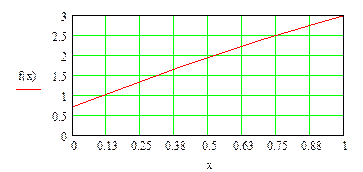
При интервале изменения коэффициента x

График имеет вид

При а=2 функция f(x)=0 имеет приближенное значения корня x=-0,25

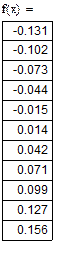
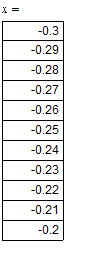
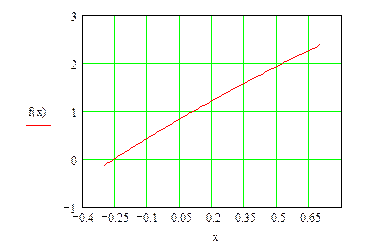
Находим более точное значение корня

-вычислительный блок

-процедура нахождения корня

-более точное значение корня

Проверка:

Нахождение более точного значения корня при помощи root

-приближенное значение корня

Находим min и max функции

-шаг изменения аргумента

- на интервале от -10 до 10

- на интервале от -10 до 10

Разложение функции d(x)=exp(x) в степенной ряд

- интервал изменения аргумента