Реферат: Задачи эконометрики в области социально-экономических исследований
3. Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, имеется набор объясняемых переменных, связанных через уравнения системы. Примером может служить модель спроса и предложения. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для моделей страновой экономики и др.
При моделировании экономических процессов мы встречаемся с двумя типами данных:
· пространственные данные;
· временные ряды.
Примером пространственных данных является, например, набор сведений (объем производства, количество работников, доход и др.) по разным фирмам в один и тот же момент времени (пространственный срез). Другим примером могут являться данные по курсам покупки/продажи наличной валюты в какой-то день по обменным пунктам города.
Примерами временных данных могут быть ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы или, например, ежедневный курс доллара США на ММВБ, цены фьючерсных контрактов на поставку доллара США (ММБ) и котировки ГКО (ММВБ) за два последних года.
Отличительной чертой временных данных является то, что они естественным образом упорядочены по времени, кроме того наблюдения в близкие моменты времени часто бывают зависимыми.
Процесс эконометрического моделирования происходит в течение нескольких этапов. В основе первого этапа статистического изучения связей лежит качественный анализ явления, связанный с анализом его природы методами экономической теории, социологии, конкретной экономики. Второй этап – построение модели связи. Он базируется на методах статистики: группировки, средних величин, таблиц и т.д. Третий этап – интерпретация результатов. Он вновь связан с качественными особенностями изучаемого явления.
Существует множество методов изучения связей, выбор конкретного из которых зависит от цели исследования и от поставленной задачи. Связи между признаками и явлениями классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса:
1. Факторные (факторы) – это признаки, обусловливающие изменение других, связанных с ними признаков.
2. Результативные – это признаки, изменяющиеся под действием факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению (выделяют прямую и обратную связь), по аналитическому выражению (выделяют прямолинейные – или просто линейные – и нелинейные - или криволинейные ).
Для выявления наличия связи, ее характера и направления используются следующие методы: метод приведения параллельных данных (основан на сопоставлении двух или нескольких рядов статистических величин, что позволяет установить наличие связи и получить представление о ее характере), аналитических группировок, графический, корреляции и регрессии.
Парная регрессия и корреляция в эконометрических исследованиях.
2.1. Основные понятия и определения.
Парная регрессия – уравнение связи двух переменных y и x :
![]()
где y – зависимая переменная (результативный признак);
x – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии. Линейная регрессия : y = a + bx + e . Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
· полиномы разных степеней y = a + b 1 x + b 2 x 2 + b 3 x 3 + e ;
· равносторонняя гипербола ![]()
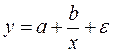 .
.
Регрессии, нелинейные по оцениваемым параметрам:
· степенная y = a × xb × e ;
· показательная y = a × bx × e;
· экспоненциальная y = e a + b × x × e .
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических ![]() минимальна, т.е.
минимальна, т.е.
![]() .
.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b :
![]()
![]()
Можно воспользоваться готовыми формулами, которые вытекают из этой системы: ![]()
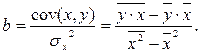
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r xy для линейной регрессии (-1 £ rxy £1 ):