Реферат: Задачі нелінійного програмування. Деякі основні методи їх розвязування та аналізу

Розв’язок . Найдем градієнт функції

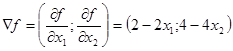
і в якості даного допустимого розв’язку задачі візьмемо точку а в якості критерія оцінки якості одержимо розв’язок – нерівності де .

1. Ітерація . В точці градієнт .Знаходимо максимальне значення функції

(65)

при умовах (63) і (64)

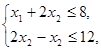(66)

(67)

Задача (65)—(67) має оптимальний план .

Найдемо новий допустимий розв’язок даної задачі по формулі (61):

, де . (68)

Підставимо замість і їх значення , отримаємо

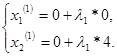(69)

Знайдемо тепер число . Підкладемо в рівність (62) замість і

із значення у відповідності з відношенням (69)

,

знайдемо подібну цій функції по і прирівняємо її нулю :

.Розв’язуючи цю рівність , отримаємо .

Оскільки найдене значення заключне між 0 і 1 , приймаючи його за величину кроку .Таким образом ,

.

2. Ітерація . Градієнт цільової функції даної задачі в точці є . Находимо максимальне значення функції при умовах (63) і (64) . Рішення являється .

Оприділяєм тепер .Останню рівність перепишемо наступним образом :

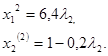
Підкладемо тепер в функцію (62) замість і їх значення у відношенні з відношенням (70) , отримаємо

звідки . Прирівняємо нулю і розв’язуючи отримаємо рівність , знаходимо . Таким образом ,

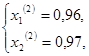
т.е. .

3. Ітерація . Градієнт функції f в точці є . Находимо максимальне значення функції при умовах (63) і (64). Розв’язком буде .

Знайдемо . Маємо