Реферат: Золотое сечение

Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".

3. Построение пропорции.

????? ?????????? ?????????? ????? ?, ??????? ??????? ?????? ? ????????? ??????? ???????.

Рис. 1. Деление отрезка прямой по золотому сечению. BC = 1/2 AB ; CD = BC

Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.

Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.

4. Второе золотое сечение.

Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

Рис. 2. Построение второго золотого сечения

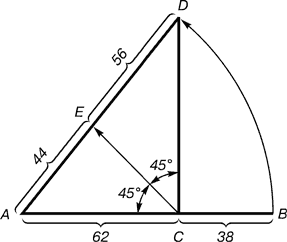
Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.

На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Рис. 3. Деление прямоугольника линией второго золотого сечения

Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.

5. "Золотые" фигуры.

5.1.Золотой прямоугольник:

Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.

Чтобы убедиться в этом, заметим, что по теореме Пифагора

МС² =а² +(а/2)² =5а² /4

В силу чего

Рис 20 стр74

??=?/2 +??=(√5+1)?/2=φ??

Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.

Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?

5.2.Золотой треугольник:

Проводим прямую АВ. От точки А

откладываем на ней три раза отрезок О

произвольной величины, через

полученную точку Р проводим перпендикуляр к линии