Реферат: Зубчатые механизмы

Окружности диаметров d ₁ (d ₂ ), полученные в результате пересечения делительных и дополнительных конусов шестерни (колеса), называются делительными окружностями конических колес. По этим окружностям определяется модуль зацепления конических колес. Его назначают из конструктивно-технических условий изготовления и сборки или по данным расчета на прочность. Зубчатый венец ограничивается внешним и внутренним торцами. Зубья конических колес по длине имеют переменную высоту и толщину. Стандартизованы размеры зубьев, их модуль и шаг по наружному торцу и обозначаются они с индексом е (m_e , p_e , d_е , d_{а е} , d_fe ).

Передаточное отношение i конической передачи определяют из условия качения без проскальзывания начальных конусов. Отсюда i = d₂ /d₁ = sinδ₂ /sinδ₁ или при Σ = 90° i = tgδ₂ = ctgδ₁ . Величину передаточного числа u для кинематических передач рекомендуется принимать не больше 7,5, для силовых – не более 3 (u = z₂ /z₁ ).

Геометрический расчет конической передачи (рис. 4) ведут по следующим зависимостям: внешний делительный диаметр колеса d_e = m_e z; углы делительных конусов колес δ₂ = arctgi, δ₁ = 90° – δ₂ ; внешнее конусное расстояние R_e = (m_e z)/(2sinδ); ширина зубчатого венца b = (0,25 … 0,3)R_e или b = (4 … 10)m_e ; среднее конусное расстояние R = R_e – 0,5b; средний окружной модуль m = (m_e R)/R_e ; внешняя высота головки зуба h_ae = m_e ; внешняя высота ножки зуба h_fe = (1 + c*)m_e , где коэффициент радиального зазора с* = 0,45 при m_е ≤ 0,5 или с* = 0,3 при 0,5 < m_e < 1 и с* = 0,2 при m_e ≥ 1,0; внешний диаметр вершин зубьев d_ae = d_e + 2h_ae cosδ; внешний диаметр впадин зубьев d_fe = d_e – 2h_fe cosδ. При прочностных расчетах расчетным является средний модуль m, по которому вычисляется внешний модуль m_e .

Конические колеса малых размеров (d_e < 70 мм) изготавливают со сплошным диском (рис. 5, а). При больших диаметрах для снижения массы и момента инерции в диске колеса предусматривают выточки, отверстия (рис. 5, б). Ступицу колеса располагают с противоположной стороны делительного конуса. Колеса с обратной ступицей (рис. 5, в) можно применять при условии, если ступица не выступает за пределы конуса впадин, что необходимо для выхода инструмента при нарезке зубьев.

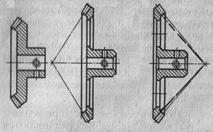
Рис. 5

Зубчатые колеса изготавливают из сталей 35, 45, 50. При требованиях малого веса и небольших нагрузках для изготовления применяются сплавы Д16Т, В95Т и пластмассы – текстолит марки ПТК, капрон. Колеса из пластмассы обеспечивают бесшумность работы.

Червячные передачи

Червячные передачи применяют, когда оси ведущего и ведомого валов перекрещиваются под углом 90°. Ведущим звеном (рис. 6.) является червяк, имеющий форму винта с соответствующим количеством ниток (заходов) z ₁ резьбы, ведомым – сопряженное с червяком червячное колесо, зубья которого имеют дугообразную форму.

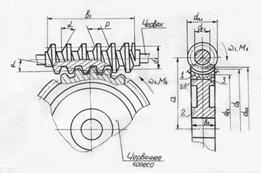
Рис. 6

Достоинством червячных передач по сравнению с зубчатыми является возможность получить большие передаточные отношения (числа) в одной ступени, до 80 в силовых передачах и до нескольких сотен в кинематических. Червячным редукторам присущи также бесшумность в работе; высокая плавность зацепления; компактность; свойство самоторможения, заключающееся в невозможности передачи вращения от колеса к червяку, что позволяет исключать из привода тормозные устройства; надежность и простота эксплуатации.

Недостатками червячных передач являются большое относительное скольжение сопряженных поверхностей в зацеплении; большие потери на трение; малый КПД; значительный нагрев зацепляющихся элементов в силовых передачах, что требует специальных мер для дополнительного охлаждения; высокая сложность и точность изготовления и сборки.

Существуют червячные передачи с цилиндрическим и глобоидным червяком . В цилиндрической передаче начальной поверхностью червяка является цилиндр, в глобоидной – поверхность, образованная вращением дуги окружности. В глобоидных передачах не только колесо, но и червяк имеют форму глобоида; за счет большего числа зубьев, находящихся одновременно в зацеплении, нагрузочная способность их на 35 … 50% больше, чем в цилиндрических, но технология изготовления значительно сложнее. Эти передачи сложны в монтаже, чувствительны к осевым смещениям червяка, в приборостроении их не применяют.

В зависимости от формы боковой поверхности витков червяка различают цилиндрические червяки с архимедовой, конволютной и эвольвентной поверхностью. Соответствующие названия червяки и передачи получили по виду кривых, получающихся в сечении витков червяка плоскостью, перпендикулярной к его оси (спираль Архимеда, удлиненная эвольвента или конволюта, классическая эвольвента окружности). В соответствии с ГОСТ 18298-73 в документации их условно обозначают ZA, ZN и ZI. Обычно применяются передачи с архимедовым и конволютным червяком. Архимедовы червяки (рис. 7, а) в осевом сечении имеют трапецеидальный профиль с углом профиля α = 20°, теоретический торцовый профиль витков является архимедовой спиралью.

Конволютные червяки имеют прямолинейный профиль витка в плоскости, нормальной к винтовой линии (рис. 7, б). Теоретический торцовый профиль витков является удлиненной или укороченной эвольвентой. Конволютные червяки применяют обычно в многозаходных передачах.

В зависимости от направления резьбы червяка различают правозаходые и левозаходные передачи, причем передачи с правозаходными червяками имеют преимущественное распространение.

В зависимости от количества параллельных витков z ₁ резьбы червяка различают одно-, двух- и четырехзаходные передачи. Передачи с z₁ = 3 используют только как специальные.

б

а

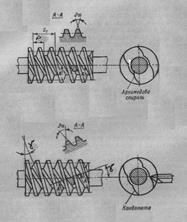
Рис. 7

По расположению оси червяка в пространстве различают передачи с горизонтальной и вертикальной осью червяка.

Исходными данными для геометрического расчета элементов червяка и червячного колеса являются: модуль зацепления m , передаточное отношение (число) i (u ), число витков (заходов) z ₁ червяка и коэффициент q диаметра червяка.

В осевом сечении витки червяка имеют форму зубчатой рейки со стандартным модулем m. Для нормальной работы необходимо, чтобы осевой шаг р = πm червяка и окружной шаг червячного колеса были равны.

Значения параметров m и q назначаются в зависимости от заданных при проектировании условий. Приведем рекомендуемый стандартом ряд модулей для червячных передач в миллиметрах: 0,20; 0,25; 0,315; 0,40; 0,50; 0,63; 0,80; 1,0; 1,25; 1,60; 2,0; 2,25; 2,5; 2,75; 3,0; 3,5; 4,0; 5,0.

Коэффициент q характеризует число модулей, содержащихся в делительном диаметре d ₁ червяка (q = d₁ /m). Рекомендуется следующий ряд значений коэффициентаq диаметра червяка: 6,3; 8,0; 10; 12,5; 16; 20;25. В случае недостаточной жесткости червяка, что характерно для мелкомодульных передач, увеличивают q ; для получения высокого КПД стремятся принимать наименьшие значения q . Рекомендуют принимать: q = 25 при m ≤ 0,8; q = (20; 25) при m = 1,0; q = (12,5; 16; 20) при m = 1,25. Для приборных передач принимают q = 16 … 25, для силовых – по ГОСТ 2144-93.

Передаточное отношение назначают по заданным условиям, учитывая, что посредством одноступенчатой червячной передачи можно получить передаточное число u в кинематических передачах до 300 и более, в силовых – до 80. Передаточное отношение может быть как целым, так и дробным. За один оборот червяка с числом заходов z ₁ червячное колесо повернется на то же число зубьев, поэтому i = u = z₂ /z₁ .

При малых значениях передаточного отношения применяют многозаходные червяки, а при больших передаточных отношениях в целях снижения размеров передачи принимают z₁ = 1 – 2. Отметим, что с увеличением величины z ₁ снижается точность передачи и увеличивается КПД. Геометрические размеры червяка следующие: делительный диаметр d₁ = mq; диаметр вершин витков d_{a 1} = d₁ + 2m; высота головки витка h_{a 1} = m; высота ножки витка h_{f 1} = 1,2m; высота витка h₁ = 2,2m; длина нарезанной части червяка b₁ ≥ (11 + 0,06z₂ )m.

Рассмотрим соотношение между геометрическими параметрами червяка (рис. 8). Развернем на плоскость делительный цилиндр диаметром d ₁ , разрезав его вдоль образующей. Нить резьбы займет положение гипотенузы ОВ₁ треугольника ОВВ₁ .Горизонтальный катет равен развертке окружности диаметра d₁ (ОВ = πd₁ ). Угол подъема γ линии витка резьбы червяка равен

tgγ = S₁ /πd₁ = pz₁ /πmq = πmz₁ /πmq = z₁ /q, (2)

где р – осевой шаг червяка; S₁ = z₁ p – ход резьбы червяка. От угла γ зависит КПД передачи, обычно γ = 2 … 26°. Величину КПД при ведущем червяке определяют по формуле

η = [(0,95 … 0,97)tgγ]/[tg(γ + φ)], (3)