Статья: О физической значимости векторных потенциалов в классической электродинамике
(c) rot![]() , (d) div
, (d) div![]() .
.
Сделаем общее для всех систем замечание о дивергентных уравнениях. Как уже говорилось, уравнение div![]() = 0 являются калибровкой, обеспечивающей однозначность функции векторного потенциала
= 0 являются калибровкой, обеспечивающей однозначность функции векторного потенциала ![]() , поэтому, согласно симметрии уравнений в рассматриваемых системах, другие дивергентные уравнения: (1b) при
, поэтому, согласно симметрии уравнений в рассматриваемых системах, другие дивергентные уравнения: (1b) при ![]() , (1d), (8b) и (9b) математически также следует считать соответствующими калибровками для функций вихревых полей
, (1d), (8b) и (9b) математически также следует считать соответствующими калибровками для функций вихревых полей ![]() и
и ![]() .
.
С точки зрения эффективности анализа физического содержания всех представленных уравнений укажем на явную предпочтительность использования в электродинамике системы единиц физических величин СИ в сравнении с абсолютной системой единиц СГС. Размерность в системе СИ множителя e0 в материальных соотношениях (2) для ![]() действительно оправдана, поскольку тем самым объединяются физически различные электрические величины: линейный (силовой) вектор напряженности
действительно оправдана, поскольку тем самым объединяются физически различные электрические величины: линейный (силовой) вектор напряженности ![]() и потоковый вектор смещения
и потоковый вектор смещения ![]() . Аналогично, в другом соотношении (2) размерная константа m0 связывает линейные и потоковые векторные величины:
. Аналогично, в другом соотношении (2) размерная константа m0 связывает линейные и потоковые векторные величины: ![]() . Напротив, в гауссовой системе единиц безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы
. Напротив, в гауссовой системе единиц безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы ![]() и
и ![]() ,
, ![]() и
и ![]() сущностно тождественными, что обедняет физическое содержание соотношений электромагнетизма, оголяя в них формализм “математики”. Физические свойства указанных полей, акцентируемые системой СИ, наиболее полно отражены в электродинамических уравнениях Максвелла (1), где, и Максвелл это особо подчеркивал [1], описываются вихри именно линейных векторов
сущностно тождественными, что обедняет физическое содержание соотношений электромагнетизма, оголяя в них формализм “математики”. Физические свойства указанных полей, акцентируемые системой СИ, наиболее полно отражены в электродинамических уравнениях Максвелла (1), где, и Максвелл это особо подчеркивал [1], описываются вихри именно линейных векторов ![]() и
и ![]() , а дивергенция потоковых
, а дивергенция потоковых ![]() и
и ![]() . Кстати, векторные потенциалы
. Кстати, векторные потенциалы ![]() и
и ![]() по определению являются линейными векторами, а векторы отклика среды на их воздействие
по определению являются линейными векторами, а векторы отклика среды на их воздействие ![]() и
и ![]() - потоковыми.
- потоковыми.
Судя по симметрии, представленные здесь системы уравнений физически не менее значимы, чем традиционная система (1), поскольку в их структуре также заложено принципиальное неразрывное единство полей электрического ![]() и магнитного
и магнитного ![]() векторных потенциалов в системе (7), полей электрической напряженности
векторных потенциалов в системе (7), полей электрической напряженности ![]() и ее вектор-потенциала
и ее вектор-потенциала ![]() в системе (8), и, наконец, полей магнитной напряженности
в системе (8), и, наконец, полей магнитной напряженности ![]() и ее вектор-потенциала
и ее вектор-потенциала ![]() в системе (9). При этом каждая из систем вполне автономна и самодостаточна при описании определенного класса физических явлений, строгое обоснование достоверности которых возможно в рамках именно этой конкретной системы электродинамических уравнений Максвелла, понимаемых теперь в значительно более широком смысле. Как видим, полученные результаты несомненно перспективны в плане непосредственного развития физических представлений о роли и месте векторных потенциалов в явлениях электромагнетизма.
в системе (9). При этом каждая из систем вполне автономна и самодостаточна при описании определенного класса физических явлений, строгое обоснование достоверности которых возможно в рамках именно этой конкретной системы электродинамических уравнений Максвелла, понимаемых теперь в значительно более широком смысле. Как видим, полученные результаты несомненно перспективны в плане непосредственного развития физических представлений о роли и месте векторных потенциалов в явлениях электромагнетизма.
Проведем анализ полученных выше систем уравнений, специфика которых состоит в том, что, являясь модификацией уравнений Максвелла электромагнитных полей, они справедливы теперь в таких областях пространства, где присутствуют одновременно поля и их векторные потенциалы, либо только потенциалы. Согласно структуре представленных уравнений, описываемые ими поля распространяются в пространстве в виде волн, скорость которых в отсутствие поглощения определяется электрическими и магнитными параметрами этого пространства: ![]() . В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение той же системы. В качестве иллюстрации получим, например, для системы (7) волновое уравнение относительно
. В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение той же системы. В качестве иллюстрации получим, например, для системы (7) волновое уравнение относительно ![]() :
:
rot rot![]() grad div
grad div![]() rot
rot![]()
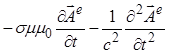 ,
,
где, согласно (7b), div![]() , а Δ – оператор Лапласа. Таким образом, имеем теперь волновые уравнения не только для электромагнитных полей
, а Δ – оператор Лапласа. Таким образом, имеем теперь волновые уравнения не только для электромагнитных полей ![]() и
и ![]() , но и для их векторных потенциалов
, но и для их векторных потенциалов ![]() и
и ![]() в парных комбинациях этих четырех уравнений в зависимости от системы. В итоге возникает физически очевидный, принципиальный вопрос: какие это волны, и что они переносят? Другими словами, необходимо прояснить физическое содержание рассматриваемых здесь систем электродинамических уравнений.
в парных комбинациях этих четырех уравнений в зависимости от системы. В итоге возникает физически очевидный, принципиальный вопрос: какие это волны, и что они переносят? Другими словами, необходимо прояснить физическое содержание рассматриваемых здесь систем электродинамических уравнений.
В случае системы (8) введем аналогично вектору Пойнтинга плотности потока электромагнитной энергии ![]() другой потоковый вектор
другой потоковый вектор ![]() , который, судя по размерности, определяет электрическую энергию, приходящуюся на единицу площади поверхности. Для аргументированного обоснования возможности существования такого вектора воспользуемся стандартными рассуждениями, как при выводе соотношения баланса энергии электромагнитного поля (3), и из уравнений системы (8) в итоге получим:
, который, судя по размерности, определяет электрическую энергию, приходящуюся на единицу площади поверхности. Для аргументированного обоснования возможности существования такого вектора воспользуемся стандартными рассуждениями, как при выводе соотношения баланса энергии электромагнитного поля (3), и из уравнений системы (8) в итоге получим:
div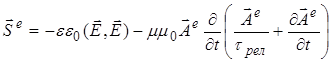 ( 10)
( 10)
- уравнение энергетического баланса процесса электрической поляризации среды в данной точке. Как видим, уравнения электрических полей напряженности ![]() и векторного потенциала
и векторного потенциала ![]() системы (8) описывают статические и динамические чисто электрические явления, показывают реальность волн, переносящих только электрическую энергию.
системы (8) описывают статические и динамические чисто электрические явления, показывают реальность волн, переносящих только электрическую энергию.
Аналогично можно ввести потоковый вектор ![]() , размерность которого определяет поверхностную плотность магнитной энергии. Подтверждение этому найдем из уравнений (9) в виде уравнения энергетического баланса процесса намагничивания среды в данной точке:
, размерность которого определяет поверхностную плотность магнитной энергии. Подтверждение этому найдем из уравнений (9) в виде уравнения энергетического баланса процесса намагничивания среды в данной точке:
div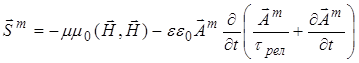 . (11)
. (11)
Следовательно, уравнения магнитных полей напряженности ![]() и векторного потенциала
и векторного потенциала ![]() системы (9) описывают статические и динамические магнитные явления, устанавливают реальность волн, переносящих только магнитную энергию.
системы (9) описывают статические и динамические магнитные явления, устанавливают реальность волн, переносящих только магнитную энергию.
Очевидно, что такие результаты анализа систем (8) и (9) в принципе невозможны и просто абсурдны в рамках традиционной электродинамики Максвелла, но это нисколько не является недостатком системы (1), а лишь иллюстрирует автономию одной системы уравнений по отношению к другим.
Полученные здесь уравнения энергетического баланса (10) и (11) описывают не только энергетику обычной электрической и магнитной поляризации среды с помощью соответствующего поля (первое слагаемое), но и показывают возможность реализации эффектов динамической поляризации вещества посредством изменяющегося во времени поля векторного потенциала, причем наличие электропроводности среды способствует этому. Надо сказать, что явления динамической поляризации вещества, как нам представляется, уже имеют реальное экспериментальное воплощение: это эффекты электродинамической индукции в металлах [7] и динамического намагничивания в ферритах и магнитоупорядоченных металлах [8, 9].
Подобным образом вводится вектор ![]() , размерность которого определяет момент импульса на единицу площади поверхности. Соответственно, уравнения (7) позволяют получить уравнение баланса процесса передачи момента импульса поля электромагнитных потенциалов в данной точке среды:
, размерность которого определяет момент импульса на единицу площади поверхности. Соответственно, уравнения (7) позволяют получить уравнение баланса процесса передачи момента импульса поля электромагнитных потенциалов в данной точке среды:
div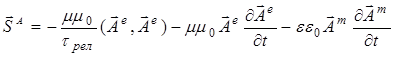 . (12)
. (12)
Согласно этому уравнению, проводящей среде момент импульса передается электрическим вектор-потенциалом, стационарным в том числе, а диэлектрической – переменными во времени полями электрического или магнитного потенциалов. Целесообразно отметить, что вектор момента импульса поля электромагнитных векторных потенциалов ![]() никак не может быть сопоставлен с предложенным в порядке гипотезы из механических аналогий вектором момента импульса электромагнитного поля
никак не может быть сопоставлен с предложенным в порядке гипотезы из механических аналогий вектором момента импульса электромагнитного поля ![]() , дискуссия о котором продолжается по сей день [6] и носит, на наш взгляд, тупиковый характер. Итак, уравнения системы (7) описывают необычные волны векторного потенциала, переносящие, согласно (12), момент электромагнитного импульса, которые, однако, в явном виде не переносят энергии, поскольку в них
, дискуссия о котором продолжается по сей день [6] и носит, на наш взгляд, тупиковый характер. Итак, уравнения системы (7) описывают необычные волны векторного потенциала, переносящие, согласно (12), момент электромагнитного импульса, которые, однако, в явном виде не переносят энергии, поскольку в них ![]() и
и ![]() равны нулю. Вопрос о физическом смысле таких волн остается открытым.
равны нулю. Вопрос о физическом смысле таких волн остается открытым.
Иллюстрацию физической значимости векторных потенциалов в электродинамике продолжим на конкретном примере использования этих понятий при анализе энергетики процесса взаимодействия металла с электромагнитным полем, где главную роль играет высокая электропроводность такой среды. Так как магнитный векторный потенциал ![]() проводника с током подробно обсуждался в работе [2], то далее наши рассуждения будут в большей степени касаться электрического векторного потенциала
проводника с током подробно обсуждался в работе [2], то далее наши рассуждения будут в большей степени касаться электрического векторного потенциала ![]() проводника с током. Такая инициатива возможна, поскольку в процессе электропроводности однородная проводящая среда остается обычно локально электронейтральной [10, 9], а потому электрическое поле в ней описывается соотношением div
проводника с током. Такая инициатива возможна, поскольку в процессе электропроводности однородная проводящая среда остается обычно локально электронейтральной [10, 9], а потому электрическое поле в ней описывается соотношением div![]() . Следовательно, выражение (4b) справедливо и в данном случае.
. Следовательно, выражение (4b) справедливо и в данном случае.
Выражение ![]() rot
rot![]() в применении к проводнику с током для большей наглядности и математической общности представим в интегральной форме:
в применении к проводнику с током для большей наглядности и математической общности представим в интегральной форме:
![]()
![]() , (13)
, (13)
где циркуляция вектора электрического потенциала ![]() по замкнутому контуру С равна потоку вектора электрического смещения
по замкнутому контуру С равна потоку вектора электрического смещения ![]() через поверхность SC , опирающуюся на этот контур, то есть определяет величину поляризационного заряда
через поверхность SC , опирающуюся на этот контур, то есть определяет величину поляризационного заряда ![]() , индуцированного на этой поверхности. Вопрос об электрической поляризации металлического проводника в процессе электропроводности подробно обсуждался в работе [11].
, индуцированного на этой поверхности. Вопрос об электрической поляризации металлического проводника в процессе электропроводности подробно обсуждался в работе [11].
На основе (13) нетрудно получить конкретные формулы связи поля вектора ![]() с полями векторов
с полями векторов ![]() и
и ![]() , при их однородном распределении внутри кругового цилиндрического проводника радиуса R и ориентированными вдоль его оси симметрии. В результате имеем:
, при их однородном распределении внутри кругового цилиндрического проводника радиуса R и ориентированными вдоль его оси симметрии. В результате имеем:
при r < R ![]()
и при r > R 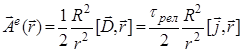 . (14)
. (14)
Таким образом, поле электрического векторного потенциала ![]() существует как в самом проводнике с током, так и вовне, оно непрерывно на его поверхности. В этой связи физически интересно представить проводник с током как “электрический соленоид”, поскольку поля индукции
существует как в самом проводнике с током, так и вовне, оно непрерывно на его поверхности. В этой связи физически интересно представить проводник с током как “электрический соленоид”, поскольку поля индукции ![]() и ее векторного потенциала
и ее векторного потенциала ![]() функционально эквивалентны аналогичным зависимостям
функционально эквивалентны аналогичным зависимостям ![]() и
и ![]() магнитного соленоида [2].
магнитного соленоида [2].
Однако представления о вектор-потенциале ![]() будут по-настоящему физически содержательными только тогда, когда указан хотя бы в принципе метод его наблюдения, а лучше конкретный способ измерения параметров такого векторного поля. В нашем случае это вполне возможно и, в соответствии с соотношением (6), электрический векторный потенциал в асимптотике низких частот (
будут по-настоящему физически содержательными только тогда, когда указан хотя бы в принципе метод его наблюдения, а лучше конкретный способ измерения параметров такого векторного поля. В нашем случае это вполне возможно и, в соответствии с соотношением (6), электрический векторный потенциал в асимптотике низких частот (![]() ) определяется посредством соотношения:
) определяется посредством соотношения:
![]() . (15)
. (15)
Видно, что распределение поля векторного электрического потенциала ![]() проводника с током полностью соответствует топологии распределения напряженности магнитного поля
проводника с током полностью соответствует топологии распределения напряженности магнитного поля ![]() , созданного этим током в процессе электропроводности, а их величины между собой прямо пропорциональны. Согласно [12], порядок величины времени релаксации электрического заряда в металлах
, созданного этим током в процессе электропроводности, а их величины между собой прямо пропорциональны. Согласно [12], порядок величины времени релаксации электрического заряда в металлах ![]() ~ 10-6 с, а конкретно для меди из эксперимента
~ 10-6 с, а конкретно для меди из эксперимента ![]() ~ 3,6·10-6 с [13]. Следовательно, электрический векторный потенциал
~ 3,6·10-6 с [13]. Следовательно, электрический векторный потенциал ![]() проводника с током при
проводника с током при ![]() можно считать косвенно наблюдаемой физической величиной, поскольку реальное измерение магнитного поля не представляет серьезной технической проблемы.
можно считать косвенно наблюдаемой физической величиной, поскольку реальное измерение магнитного поля не представляет серьезной технической проблемы.