Статья: Солнечный ветер
Таким образом, решение уравнения (8) на больших расстояниях имеет две ветви: верхнюю (![]() ) и нижнюю (
) и нижнюю (![]() ). Для того чтобы выбрать решение, приемлемое с физической точки зрения, вычислим плотность плазмы, соответствующую этим решениям.
). Для того чтобы выбрать решение, приемлемое с физической точки зрения, вычислим плотность плазмы, соответствующую этим решениям.
Из равенства (4) следует
| (10) |
Подставляя в (10) величину ![]() из (9а), (9б), находим
из (9а), (9б), находим
 | (11) |
Из равенств (11) видно, что в случае, когда ![]() соответствует нижней ветви решения, плотность плазмы при
соответствует нижней ветви решения, плотность плазмы при ![]() стремится к конечной и относительно большой величине, что противоречит экспериментальным данным. В то же время верхняя ветвь решения соответствует
стремится к конечной и относительно большой величине, что противоречит экспериментальным данным. В то же время верхняя ветвь решения соответствует ![]() , что удовлетворяет условиям модели. Таким образом, на больших расстояниях от Солнца физический смысл имеет лишь верхняя ветвь решения уравнения Паркера.
, что удовлетворяет условиям модели. Таким образом, на больших расстояниях от Солнца физический смысл имеет лишь верхняя ветвь решения уравнения Паркера.
Малые расстояния (![]() )
)
При ![]() третий член в левой части равенства (8) неограниченно возрастает. Поскольку в правой части уравнения постоянная величина, это означает, что неограниченное возрастание
третий член в левой части равенства (8) неограниченно возрастает. Поскольку в правой части уравнения постоянная величина, это означает, что неограниченное возрастание ![]() должно быть скомпенсировано одним из первых двух членов в левой части (8), то есть опять имеют место две ветви решения:
должно быть скомпенсировано одним из первых двух членов в левой части (8), то есть опять имеют место две ветви решения:
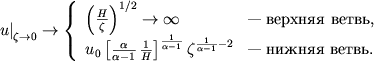 | (12) |
Первое решение, соответствующее неограниченному возрастанию скорости солнечного ветра при ![]() , физически неприемлемо. Второе решение дает разумный результат
, физически неприемлемо. Второе решение дает разумный результат ![]() при значениях показателя политропы, определяемых неравенством
при значениях показателя политропы, определяемых неравенством ![]() , то есть
, то есть ![]() .
.
Таким образом, стационарное решение короны оказывается возможным лишь в том случае, если показатель политропы a меньше адиабатического (![]() = 5/3), то есть если имеет место непрерывный приток энергии в корону и солнечный ветер. В первоначальной модели Паркера предполагалось, что необходимый приток энергии обеспечивается высокой теплопроводностью солнечной плазмы. Однако, как будет показано ниже, одного лишь потока тепловой энергии недостаточно для ускорения солнечного ветра, и требуются дополнительные источники энергии.
= 5/3), то есть если имеет место непрерывный приток энергии в корону и солнечный ветер. В первоначальной модели Паркера предполагалось, что необходимый приток энергии обеспечивается высокой теплопроводностью солнечной плазмы. Однако, как будет показано ниже, одного лишь потока тепловой энергии недостаточно для ускорения солнечного ветра, и требуются дополнительные источники энергии.
Итак, мы видим, что физически разумным граничным условиям при больших ![]() удовлетворяет верхняя ветвь решения уравнения Паркера, а при малых
удовлетворяет верхняя ветвь решения уравнения Паркера, а при малых ![]() - нижняя. Сращивание этих двух ветвей решения зависит от поведения решения в окрестностях некоторой критической точки, положение которой на плоскости
- нижняя. Сращивание этих двух ветвей решения зависит от поведения решения в окрестностях некоторой критической точки, положение которой на плоскости ![]() определяется следующим образом.
определяется следующим образом.
Продифференцируем уравнение (8) по ![]() :
:
| (13) |
Определим критическую точку (![]() ) как точку, где правая часть уравнения (13) и коэффициент при
) как точку, где правая часть уравнения (13) и коэффициент при ![]() в левой части уравнения одновременно равны нулю. Тогда
в левой части уравнения одновременно равны нулю. Тогда
| (14) |
Топология решения уравнения (8) в окрестностях критической точки показана на рис. 1. Решение представляет собой семейство гипербол. При этом существует лишь одно решение, удовлетворяющее граничным условиям как на больших, так и на малых расстояниях от Солнца. Этому решению соответствует кривая, проходящая через критическую точку (критическое решение).
 |
| Рис. 1. Семейство кривых решения уравнения Паркера в окрестности критической точки. |
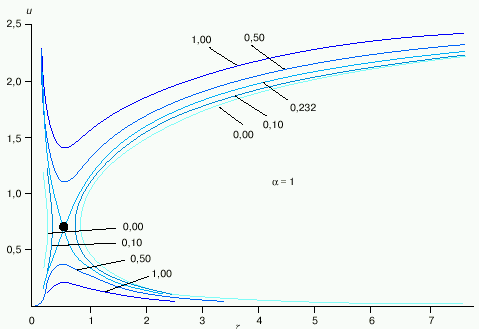
Радиальные профили скорости солнечного ветра в случае изотермической (![]() = 1) короны при различной температуре последней представлены на рис. 2. Из приведенных кривых видно, что решение достаточно чувствительно к граничным условиям. Так, например, при Т0 = 0,5 106 К скорость солнечного ветра на орбите Земли оказывается равной 260 км/с, а при T = 4 106 К - около 1150 км/с, что в целом не противоречит экспериментальным данным (см. табл. 1 из [4]). В то же время рассчитанная плотность плазмы на орбите Земли 25-40 см- 3 вместо реальных 5-10 см- 3.
= 1) короны при различной температуре последней представлены на рис. 2. Из приведенных кривых видно, что решение достаточно чувствительно к граничным условиям. Так, например, при Т0 = 0,5 106 К скорость солнечного ветра на орбите Земли оказывается равной 260 км/с, а при T = 4 106 К - около 1150 км/с, что в целом не противоречит экспериментальным данным (см. табл. 1 из [4]). В то же время рассчитанная плотность плазмы на орбите Земли 25-40 см- 3 вместо реальных 5-10 см- 3.
 |
| Рис. 2.Радиальные профили скорости солнечного ветра в модели Паркера при различных температурах T короны. |
Как видно из таблицы, скорость солнечного ветра меняется в достаточно широком диапазоне - от ~ 300 до ~ 700 км/с. Казалось бы, эти вариации легко объяснимы в рамках модели Паркера соответствующими вариациями температуры короны (см. рис. 2). Однако непосредственные наблюдения свидетельствуют, что источником рекуррентных высокоскоростных потоков являются корональные дыры (см. ниже), в которых температура короны существенно ниже средней. В связи с этим обратим внимание на то, что, согласно модели, скорость солнечного ветра помимо температуры короны зависит также от величины показателя политропы ![]() : чем больше
: чем больше ![]() , тем меньше скорость солнечного ветра на орбите Земли. Наилучшее соответствие между модельными расчетами и экспериментальными данными получено Паркером при
, тем меньше скорость солнечного ветра на орбите Земли. Наилучшее соответствие между модельными расчетами и экспериментальными данными получено Паркером при ![]() = 1,1 вблизи Солнца и
= 1,1 вблизи Солнца и ![]() = 5/3 на больших расстояниях от него.
= 5/3 на больших расстояниях от него.
Однако в связи с малой величиной показателя ![]() возникает затруднение следующего рода: при
возникает затруднение следующего рода: при ![]() градиент температуры
градиент температуры ![]() . При этом поток тепла, обусловленный теплопроводностью, также стремится к нулю. Таким образом, для поддержания достаточно высокой температуры солнечного ветра требуются дополнительные нетепловые источники энергии, связанные, скорее всего, с диссипацией энергии альфвеновских волн [3].
. При этом поток тепла, обусловленный теплопроводностью, также стремится к нулю. Таким образом, для поддержания достаточно высокой температуры солнечного ветра требуются дополнительные нетепловые источники энергии, связанные, скорее всего, с диссипацией энергии альфвеновских волн [3].
Вклад МГД-волн в тепловую энергию и импульс солнечного ветра обсуждаются в ряде публикаций. Обзор этих исследований и их дальнейшее развитие даны И. Чашеем и В. Шишовым (1987 год). Выбрав соответствующим образом интенсивность и спектр МГД-волн в основании короны, можно получить не только соответствующую экспериментальным данным скорость солнечного ветра на орбите Земли, но и необходимую плотность плазмы.
Вместе с тем модель, развиваемая в рамках одножидкостной гидродинамики, не в состоянии объяснить наблюдаемую разность электронной и ионной температур в солнечном ветре (см. табл. 1).
Таблица 1. Параметры солнечного ветра на орбите Земли
| Параметр, размерность | Средняя величина | Солнечный ветер | |
| медленный | высоко скоростной | ||
| n, см-3 | 8,7 | 11,9 | 3,9 |
| 468 | 327 | 702 | |
| n | 3,8 | 3,9 | 2,7 |
| Tp , К | 7 | 3,4 | 2,3 |
| Te , К | 1,4 | 1,3 | 1,0 |
| Te / Tp | 1,9 | 4,4 | 0,45 |
Следует заметить, что одножидкостные модели гидродинамики применимы в физике плазмы лишь в том случае, когда частота столкновений электронов с ионами достаточно велика, что обеспечивает эффективный обмен импульсом между электронной и ионной компонентами плазмы и соответственно равенство их температур. P.A. Sturrock и R.E. Hartle (1966 год) обратили внимание на то, что в солнечном ветре вследствие быстрого убывания плотности плазмы с расстоянием от Солнца последнее условие может не выполняться и температура ионов может существенно отличаться от температуры электронов. При этом, поскольку ионная теплопроводность относительно мала, протонная компонента короны Солнца расширяется почти адиабатически и соответственно быстро охлаждается. В то же время теплопроводность электронной компоненты плазмы относительно велика, в связи с чем температура последней падает с расстоянием достаточно медленно, что в целом не противоречит экспериментальным данным (см. табл. 1).
Такое относительно независимое существование электронной и ионной компонент плазмы описывается в рамках двухжидкостной гидродинамики. При этом в уравнении движения (3) газовое давление следует заменить суммой давлений электронного и ионного газов P = Pe + Pi = nk(Te + Ti ). Кроме того, в случае двухжидкостной гидродинамики уравнение газового состояния обычно заменяют уравнением сохранения энергии, записанным отдельно для электронной и ионной компонент, так что система уравнений (2) - (4) принимает вид [1]
| | (15) |
| (16) |
| (17) | |
| (18) | |
здесь ![]() и
и ![]() - масса иона и электрона соответственно,
- масса иона и электрона соответственно, ![]() и
и ![]() - ионная и электронная температура;
- ионная и электронная температура; ![]() - коэффициент ионной (электронной) теплопроводности,
- коэффициент ионной (электронной) теплопроводности, ![]() - постоянная Больцмана и
- постоянная Больцмана и ![]() - частота столкновений ионов с электронами.
- частота столкновений ионов с электронами.
Результаты численного интегрирования системы уравнений (15)- (18) представлены на рис. 3 из [1] . Кривая 1 соответствует одножидкостной модели, кривые 2 и 3 показывают изменение с расстоянием электронной и ионной температуры солнечного ветра в двухжидкостной модели. Как видно из рисунка, на орбите Земли (r = 215![]() Tp = 4,4 103 K и Te = 3,4 105 K.
Tp = 4,4 103 K и Te = 3,4 105 K.
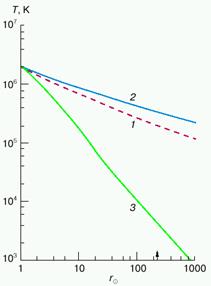 |
| Рис. 3. Изменение с расстоянием от Солнца |
Таким образом, предсказываемая моделью температура электронов оказывается вдвое больше, а температура протонов - на порядок меньше реальной температуры частиц в солнечном ветре (см. табл. 1). Такое несоответствие теоретических и экспериментальных данных можно устранить, предположив существование дополнительных источников нагрева плазмы, причем преимущественно ее ионной компоненты. Этому требованию удовлетворяют упомянутые выше альфвеновские волны. Дело в том, что, хотя сами альфвеновские волны в солнечном ветре почти не поглощаются, они эффективно трансформируются в ходе четырехволнового взаимодействия в магнитозвуковые волны. Последние же в условиях, характерных для солнечного ветра, диссипируют в результате резонансного взаимодействия с протонами, которые при этом заметно нагреваются.
Параметры солнечного ветра на орбите Земли, полученные A. Barnes и др. в 1971 году в рамках двухжидкостной модели с учетом дополнительного источника энергии в виде МГД-волн, представлены в табл. 2.
Таблица 2. Параметры солнечного ветра на орбите Земли в двухжидкостной модели Барнеса
| Плотность плазмы n, см-3 | 15 |
| Скорость | 330 |
| Поток кинетической энергии, эрг | 0,46 |
| Протонная температура Tp , K | 3,2 |
| Электронная температура Te , K | 2,2 |
| Отношение Te / Tp | 6,9 |
Рассчитанные параметры солнечного ветра на орбите Земли оказываются близкими к наблюдаемым параметрам медленного солнечного ветра (см. табл. 1). В то же время параметры высокоскоростных потоков в солнечном ветре заметно отличаются от предсказываемых моделью. В частности, температура протонов в этих потоках оказывается выше температуры электронов, что, по-видимому, свидетельствует о повышенной интенсивности альфвеновских волн в области их источника на Солнце.
Рассмотрим подробнее высокоскоростной солнечный ветер и обсудим его возможные источники.
Высокоскоростной солнечный ветер
Как видно из данных, представленных в табл. 1, высокоскоростной солнечный ветер характеризуется повышенной скоростью (около 700 км/с), пониженной плотностью плазмы (n = 4 см-3) и повышенной ионной температурой. Однако, прежде чем обсуждать возможные источники этих потоков, напомним, что существуют по меньшей мере два рода таких потоков: рекуррентные и спорадические.