Статья: Устойчивость упругих систем

где частоты связаны с волновыми числами дисперсионным соотношением .

Заметим[3] , что , при любом значении .

В свою очередь, линеаризованное уравнение для изгибных волн принимает вид

(5) .

Очевидно, что в правой части уравнения (5) содержится пространственно-временной параметр в форме суперпозиции стоячих волн.

Учет "волны параметра" становится принципиальным, если типичная скорость продольных волн оказывается сравнимой с групповыми скоростями изгибных волн.

В противном случае можно, формально полагая, что или , ограничиться изучением следующей простейшей модели:

(6) ,

которая описывает лишь только параметрическое возбуждение системы во времени. Решение уравнения (5) можно построить с помощью метода Бубнова-Галеркина: , где - волновые числа изгибных волн; - амплитуды, определяемые из решения системы обыкновенных уравнений

(7) .

Здесь

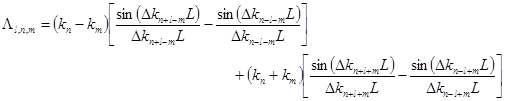
коэффициент, содержащий параметры расстройки по волновым числам, , которые, в свою очередь, не могут быть равными нулю в отсутствие резонанса; - частоты изгибных волн при , и как и прежде - критические значения силы Эйлера.

Уравнения (7) описывают раннюю стадию эволюции волн за счет многомодовых параметрических взаимодействий. Возникает ключевой вопрос о сопоставимости возмущенных орбит системы (7) и траекторий соответствующей невозмущенной подсистемы

(8) ,

которая получается из уравнений (7) при . Другими словами, - насколько эффективен динамический отклик системы (7) на малое параметрическое возбуждение? Сначала перепишем систему (7) в эквивалентной матричной форме: , где - вектор решения; - матрица собственных чисел; - квазипериодическая матрица с компонентами на основных частотах . Следуя стандартной методике теории обыкновенных дифференциальных уравнений, решение уравнений (7) ищется в той же форме, что и для уравнений (8), где константы интеграции рассматриваются как новые искомые переменные, например , где - вектор нетривиального колебательного решения линейного однородного уравнения (8), характеризуемого набором собственных чисел . После подстановки в (7) получаются уравнения первого приближения в представлении решения рядом по малому параметру : . Правые части этих уравнений очевидно представляются суперпозицией периодических функций на комбинационных частотах . Таким образом, в первом приближении решение уравнения (7) оказывается ограниченными квазипериодическими функциями[4] , когда комбинации частот ; в противном случае в системе возникают резонансы.

В нерезонансном случае можно продолжить асимптотическую процедуру нахождения решения, т.е. , для определения высших приближений к истинному решению[5] . Другими словами, мера динамического возмущения системы оказывается того же порядка, что и мера параметрического возбуждения. Напротив, в резонансном случае решение уравнений (7), вообще говоря, нельзя представить сходящимся рядом по . Следовательно, возможен эффективный отклик системы даже на очень небольшое параметрическое возбуждение. В частном случае внешнего воздействия , уравнения (7) можно весьма упростить:

(9)

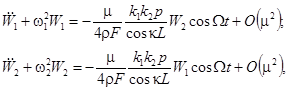
при условии, что пара изгибных волн с волновыми числами и , создает малую волновую расстройку , т.е. , и малую частотную расстройку , т.е. . Значения величин и можно также без всякого принципиального ущерба считать малыми. Выражения и можно интерпретировать как условия фазового синхронизма, необходимые для формирования резонансной тройки волн, состоящей из первичной высокочастотной продольной волны, возбуждаемой при помощи внешней гармонической силы , и вторичных низкочастотных изгибных волн, параметрически возбуждаемых за счет резонанса со стоячей продольной волной.

Заметим, что в случае упрощенной модели (6), соответствующая система амплитудных уравнений сводится к единственному уравнению типа уравнения Матье, широко применяемому во многих прикладных задачах:

Известно, что это уравнение обладает неустойчивыми решениями при малых расстойках и . Решение уравнений (7) можно найти методом Ван-дер-Поля:

(10) ; ,

где и - новые неизвестные координаты.

Подставляя это выражение в (9), получаем уравнения первого приближения:

(11) ; ,

где - коэффициент параметрического возбуждения; обобщенная фаза, удовлетворяющая следующему уравнению: 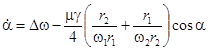. Уравнения (10) и (11), обладая гамильтоновой структурой, очевидно, обладают первыми интегралами и , позволяющими проинтегрировать систему аналитически. При существуют квазигармонические решения (10) и (11), когда , что ассоциируется с границами областей устойчивости в пространстве параметров системы.

С физической точки зрения можно утверждать, что параметрическое возбуждение изгибных волн проявляется как вырожденный случай нелинейных многоволновых взаимодействий. Это означает, что изучение резонансных свойств нелинейных свободно осциллирующих упругих систем весьма принципиально для понимания природы динамической неустойчивости.

Трехволновые резонансные взаимодействия

Свободные многочастотные нелинейные колебания бесконечно длинного тонкого прямолинейного стержня впервые изучались в работе [13], на основе уравнений модели Бернулли-Эйлера. В отличие от стандартного подхода к подобным задачам, авторы при формулировке проблемы первично выдвинули предположение о существовании фазового синхронизма между волнами: