Учебное пособие: Амплитудно-частотные характеристики и настройка связанных контуров

.

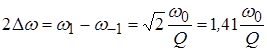Сравнивая данный результат с ПП одиночного контура, замечаем, что у связанных контуров, при критической связи ПП в раз больше. Граничные частоты ПП определяются в предположении, что резонансная характеристика обладает арифметической симметрией, т. е.

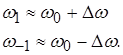
Можно показать (по аналогии с одиночным контуром), что в этом случае меньше (), т. е. избирательность лучше, чем у одиночного контура ().

Примечание. Отметим, что 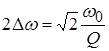и т. е. при справедливо соотношение:

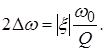
АЧХ СВЯЗАННЫХ КОНТУРОВ ПРИ СВЯЗИ БОЛЬШЕ КРИТИЧЕСКОЙ ()

В данном случае имеем три экстремальных значения АЧХ при

.

Легко понять, что здесь имеет место один минимум и два максимума:

При получим:

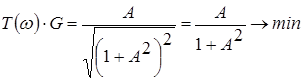(т. к. ).

При имеем:

.

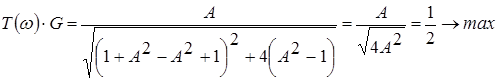График при имеет вид (рис. 2).

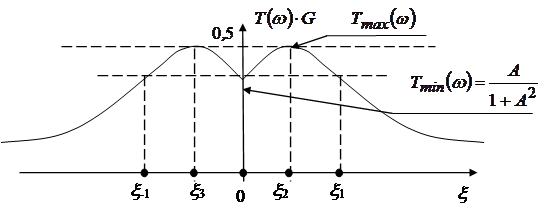
Рис. 2

Отношение 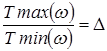называют неравномерностью АЧХ связанных контуров. Если в это выражение подставить полученные выше значения max и min АЧХ получим:

.

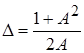Величина D зависит от параметра связи . При , т. е. неравномерность АЧХ отсутствует.

Найдем ПП связанных контуров при связи больше критической.

Т. к. ПП определяется на уровне 0,707 от максимального значения АЧХ, а , то

,

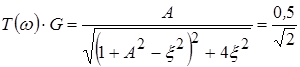и при этом неравномерность АЧХ имеет максимально допустимое значение Найдем параметр связи соответствующий этой наравномерности:

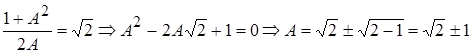
(удовлетворяет условию )

(не удовлетворяет условию ).

Подставив полученное значение в исходное соотношение для АЧХ, получим величины и , соответствующие граничным частотам ПП:

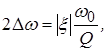и . Т. к. то ПП .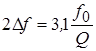

Граничные частоты ПП можно найти по приближенным формулам, отражающим арифметическую симметрию АЧХ:

и .