Дипломная работа: Анализ работы компрессорных установок
, где 
- политропный КПД i-й секции.
Используя разложение по малому параметру 
в линейном приближении, можно упростить выражение (1.4)
, (1.5)
где 
- отношение давлений секции по сечениям входа и выхода, 
- относительные потери давления. Потери, связанные с работой газоохладителей, логично оценить отношением работ компрессора с реальными и идеальными аппаратами. Под идеальными будем понимать аппараты, охлаждающие газ до температуры окружающей среды 
= 0и не имеющие гидравлических потерь
=0. Работа компрессора с идеальными охладителями при прочих равных условиях минимальна.
(1.6)
Потери, связанные с не идеальностью газоохладителей, обозначим через 
называют коэффициентом приведенных потерь охлаждения.
Для охлаждаемого многоступенчатого компрессора
(1.7)
Коэффициент приведенных потерь охлаждения компрессора для выпускаемых ныне машин лежит в диапазоне 
. Коэффициенты приведенных потерь охлаждения i-й секции 
имеют более широкий диапазон: =1.01-1.12 [1].
Выражения (1.3) - (1.7) позволяют представить изотермный КПД компрессора (1.2) в виде
(1.8)
Сомножитель 
в выражении (1.8) появляется из-за того, что изотермную
работу [см. формулу (1.3)] принято определять по температуре всасывания, тогда как минимальная работа компрессора с идеальными охладителями [см. формулу (1.6)] определена по температуре окружающей среды. В общем случае 
Если все секции одинаковы, т.е. 
и 
, то
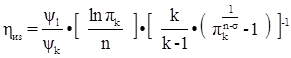, (1.9)
Умножая числитель и знаменатель на 
и вводя обозначение 
преобразуем (1.9.) к виду
(1.10)
Из формулы (1.10) видно влияние на 
различных факторов:
· числа промежуточных охлаждений n
· КПД процесса сжатия
· коэффициента приведенных потерь охлаждения
При устремлении числа охлаждений к бесконечности n
, z
и выражение (1.10) имеет своим пределом величину
, (1.11)
которая для идеальной системы охлаждения (
) становится равной 
Для иллюстрации соотношения экономии энергий от введения охлаждения и потерь, связанных с организацией, используют величину:
, (1.12)
где 
- удельная работа неохлаждаемого компрессора, в котором значение 
принято как среднее по отдельным секциям.
Полагая секции одинаковыми и используя обозначения (1.10), приведём (1.12) к виду
(1.13)