Дипломная работа: Блочно-симметричные модели и методы проектирования систем обработки данных

Пусть задано множество задач СОД РВ . Технологии решения каждой задачи соответствует направленный граф , где множество вершин графа, отражающих информационные элементы задачи ; - множество отношений между информационными элементами . Каждому графу соответствует квадратная бинарная матрица смежности размера . Элемент матрицы равен 1, если элементы и графа связаны отношениями , и равен 0 в противном случае.

Структурированный граф взаимосвязей информационных элементов задачи, преобразованный к виду, не содержащему циклов обработки, называется скелетным графом задачи . Он состоит из ряда уровней или непересекающихся подмножеств вершин, каждая из которых является выходным результатом обработки предыдущего уровня или подмножества информационных элементов. С использованием графа определяется множество процедур обработки данных, необходимых для решения задач . Для каждой упорядоченной пары элементов определим подмножества

.

Затем определим на множестве декартово произведение . Пара элементов связано с процедурой , если она принадлежит отношению . Совокупность процедур задачи образует множество . Полное множество процедур анализируемого множества задач определяется путем объединения .

Для определения в задаче входных, промежуточных и выходных данных, последовательности их получения и контуров обратной связи, а также анализа взаимосвязей в системе введено понятие матрицы достижимости.

Под матрицей достижимости понимается квадратная бинарная матрица, проиндексированная одинаковым образом по обеим осям множеством информационных элементов . Элемент достижим из элемента , если на графе можно указать направленный путь от вершины к вершине (либо ),

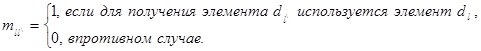
Матрица определяется на основе матрицы . При этом они связаны булевым уравнением

Анализ структур обработки данных для каждой задачи СОД и определение необходимой последовательности получение информационных элементов упрощается, если элементы построенной матрицы достижимости упорядочить по уровням (этапом) их обработки. Получение матрицы методом свертки циклов позволяет уменьшить ее размерность, облегчить анализ и синтез структуры решение как отдельных задач системы, так и функционирования всей СОД РВ.

Процесс построения матриц достижимости значительно упрощается, если проектировщик представляет информацию не о парных отношениях «информационный элемент – информационный элемент», а информацию о существовании направленного пути (путей) между парами информационных элементов.

Взаимосвязь между процедурами обработки данных при обслуживании каждой заявки СОД РВ, наборами входных и промежуточных данных удобно представлять с помощью таблицы инциденции обработки множеств запросов , которая представляет собой матрицу вида

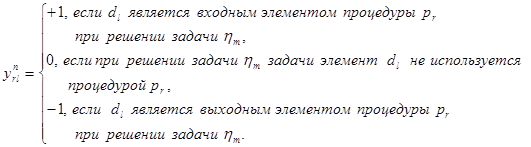
В матрице каждая строка отображает процедуру обработки, а каждый столбец – использование всеми процедурами при решении задачи рассматриваемого информационного элемента. В строке содержится информация о множестве входных и выходных данных, связанных с анализируемой процедурой. Анализ столбцов позволяет выявить входные и выходные информационные элементы рассматриваемой задачи . Элементы являются входными при решении задачи, если столбец матрицы содержит единственную, отличную от нуля запись . Если -й столбец содержит запись , то соответствующий ему элемент является выходным. Технологической матрицей смежности при решении задачи назовем квадратную бинарную матрицу, проиндексированную по обеим осям множествами . Матрица имеет четыре подматрицы: с размерами .

Нулевые элементы подматрицы соответствует элементам, равным -1 в матрице , а не нулевые элементы подматрицы соответствует элементам, равным +1 в транспонированной матрице . Таким образом, элемент матрицы равен 1, если элемент является входным для процедуры , и элемент равен 1, если элемент является входным при решении задачи. В противном случае элементы в позициях и равны 0. Единичный элемент в позиции , подматрицы соответствует наличию единичных элементов в позиции подматрицы и в позиции подматрицы , , что равносильно существованию информационного элемента , который является входным для процедуры , и выходным для процедуры при решении задачи. Для удобство формального описания будет считать, что главная диагональ подматрицы заполнена единичными записями.

Используя матрицу , можно определить матрицу , которая содержит подматрицы , проиндексированы соответственно: .

Подматрица удовлетворяет соотношению , где -целое положительное число, не больше числа элементов при решении задачи, т.е. . Матрица содержит единичные элементы в позиции , если процедура входит в последовательность процедур, необходимую для получения элемента при решении задачи. В противном случае запись в позицию подматрицы равна нулю. Подматрица определяется соотношением и содержит единичный элемент в позиции , если элемент является входным для последовательности процедур, в состав в которых входит процедура . В противном случае элемент равен 0. Подматрица является матрицей достижимости процедур обработки данных при решении задачи и удовлетворяет соотношению

.

Единичная запись в позиции подматрицы соответствует наличию направленного пути в графе технологии решения задачи от процедуры к процедуре .

Построение единого интегрированного графа осуществляется путем выполнения операции «наложения» графов и заключается в совмещении идентичных уровней каждого графа и идентичных вершин на каждом уровне. В результате формируется интегрированный граф , которому соответствует матрица смежности , , , полученная путем логического сложения матриц :

.

Анализ структур полученного интегрированного графа позволяет на заключительном этапе анализа определить следующие общесистемные требования к обслуживанию заявок в СОД РВ: множество требуемых задач обработки данных для обслуживания одного типа заявок и базовые задачи для каждого типа, взаимосвязи между заявками по решаемым задачам и между задачами по используемым процедурам и данным, рациональную дисциплину обслуживания заявок и оценку требуемой производительности вычислительной системы для заданной дисциплины обслуживания.

В качестве моделей описания и анализа задач обработки данных при создании типовых модульных СОД также используется аналогичная совокупность графовых и матричных моделей. Методика анализа и структуризация исходной для синтеза системы типовых модулей СОД информации базируется на последовательном преобразовании матричных и графовых моделей алгоритмов решения задач обработки данных, содержащих всю необходимую информацию о взаимосвязях и отношениях между различными элементами отдельных задач. При формировании полного структурированного графа технологии решения задачи учитывается наличие в алгоритмах решения задач обработки данных циклических участков и альтернативных вариантов обработки, процедур обновления информационных элементов и процедур принятия решений. Полный структурированный граф и соответствующие ему матрицы смежности и достижимости позволяют описывать алгоритмы решения задач обработки данных в целом и отдельные их части с заданной степенью детализации [31,32,34,39,40]

Рост числа решаемых и диалоге задач в составе модульных СОД их сложности, повышение требований к своевременности, достоверности и полноте представляемой информации обусловливает необходимость дальнейшего усовершенствования методологии проектирования СОД которая должна учитывать не только особенности “человеческого фактора”, но и требование по обеспечению максимальной эффективности использования технического, программного и информационного обеспечения диалоговых систем (ДС) и их типизации.

На стадии предпроектного анализа ДС необходимо выполнить комплекс работ, основной из которых также является анализ решаемых пользователями задач, технологии их решения, определения требований пользователей к эффективности и качеству решения задач [40]. На этой стадии определяется необходимый набор процедур реализации комплекса диалоговых задач и требуемой для их решения информации.

Для представления результатов изучения и анализа задач пользователей и технологии их решения используется модификации описанных выше формализованных методов представления результатов этого изучения.

Определение процедур обработки данных, анализ и структуризацию каждой диалоговой задачи целесообразно осуществлять с использованием дополнительной совокупности матричных и графовых моделей, обеспечивающих подготовку локальных сценариев (ЛС) диалога и других исходных данных, необходимых для технического проектирования оптимальных ДС [41].