Физика / Дипломная работа: Экспериментальные исследования процесса тепломассообмена и химических реакций углерода с газами

Дипломная работа: Экспериментальные исследования процесса тепломассообмена и химических реакций углерода с газами

где d – диаметр углеродной частицы, м; - предэкспоненциальный множитель, 1/с; - энергия активации реакции (ІV), Дж/моль; - температура газовой смеси, К; - коэффициент диффузии окиси углерода, м² /с; Nu – критерий Нуссельта. Малое значение критерия Семенова определяется экспериментальными условиями, когда частица дополнительно разогревается током высокой частоты или в результате поглощения лазерного излучения и обдувается холодным газом [5-7]. Так в [5] частица электродного угля d=1.2 – 1.5 см, нагреваемая током высокой частоты, обдувалась воздухом комнатной температуры (Т_g =293 К) со скоростью V=0.6 м/с. В [6-7] приведены экспериментальные и теоретические результаты временных зависимостей температуры и диаметра углеродной частицы, горение которой в воздухе комнатной температуры поддерживается лазерным излучением.

Проведенный анализ тепломассообмена и кинетики химических реакций (І), (ІІ), (ІІІ) углеродной частицы с газами показал на необходимость учета стефановского течения и позволил получить аналитические выражения качественно верно описывающие влияние условий и свойств на газовый состав продуктов реакции, скорость химического превращения углерода, плотности тепловых и массовых потоков на поверхности частицы [3]. Однако, пренебрежение внутренним реагированием привело к несовпадению экспериментальных и расчетных результатов по скорости химического превращения углеродной частицы при различных ее температурах и диаметрах.

Задачей настоящей работы является выявление роли внутреннего реагирования и стефановского течения в процессах ТМО и химических реакций пористой углеродной частицы с газами с учетом вынужденной и естественной конвекции в зависимости от температуры и диаметра частицы.

Скорость химического превращения углерода в газообразные компоненты определяется скоростью химической реакции на внешней поверхности частицы и внутри частицы на поверхностях пор

где - соответственно, суммарная скорость химического превращения, скорость химического превращения на поверхности углеродной частицы и внутри, на поверхностях пор, кг/(м² с).

Скорость химического превращения углерода на поверхности частицы определяется кинетикой реакций (I), (II) и (III)

, (2.1)

где – молярные массы углерода, кислорода, углекислого газа, кг/моль; – относительные массовые концентрации O₂ и CO₂ на поверхности частицы; , , – константы скоростей химических реакций (I), (II), (III), м/с; , , - предэкспоненциальные множители, м/с; E₁ , E₂ , Е₃ – энергии активации (I), (II) и (III) реакций, Дж/моль; R – универсальная газовая постоянная, Дж/(моль×К); Т – температура частицы, К; , - плотность газа при температуре частицы и при Т₀ =273.15 К, кг/м³ .

Энергии активации и предэкспоненциальные множители реакций (I), (II) и (III) связаны между собой [1]:

; ,

где =1 для реакции (I), 2- для реакции (II) и 3- для реакции (III).

Выражение для скорости химического превращения углерода в результате химических реакций на поверхностях пор внутри объёма частицы получается из решения задачи внутренней диффузии и может быть представлено в виде

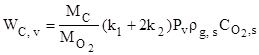, , (2)

, (3)

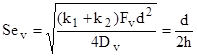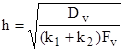, , (4)

где -эффективная константа внутреннего реагирования, м/с; Se_v - критерий Семенова, определяющий соотношение констант скоростей химических превращений на поверхностях пор и диффузии [8, 9] или отношение радиуса частицы к глубине реакционной зоны, D_v – коэффициент внутренней диффузии кислорода в порах, м² /с; - глубина реакционной зоны внутреннего реагирования, м, – удельная поверхность пор, м^-1 .

Коэффициент внутренней диффузии выражается через порозность частицы [1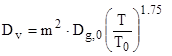, 5]

, (5)

где - коэффициент диффузии кислорода в воздухе при температуре , м² /с; - порозность частицы.

Суммарная скорость химического превращения углеродной частицы и плотность химического тепловыделения

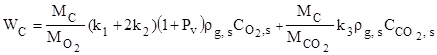, (6)

, (7)

где Q₁ , Q₂ – тепловые эффекты химических реакций (I) и (II), рассчитанные на единицу массы кислорода, Дж/кг; Q₃ – тепловой эффект реакции (III), рассчитанный на единицу массы углекислого газа, Дж/кг; - суммарная плотность химического тепловыделения, на поверхности и внутри частицы, соответственно, Вт/м² .

2.2. Взаимовлияние кинетики химических реакций и массообмена пористых углеродных частиц с газами.

Влияние относительной скорости движения частицы на кинетику химических реакций и тепломассообмен учитывается радиусом приведенной пленки , на поверхности которой задаются параметры невозмущенного потока [1, 2]. Для случая отсутствия вынужденной и естественной конвекций (частица неподвижна относительно газа, Nu=2) радиус приведенной пленки равен бесконечности. Радиус приведенной пленки уменьшается с увеличением интенсивности естественной и вынужденной конвекций, приближаясь к радиусу частицы . Зависимость от критерия Нуссельта имеет вид:

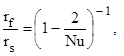(8)

, (9)

, [5, 10]

, , , ,

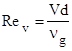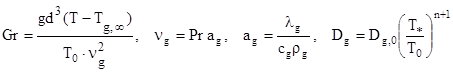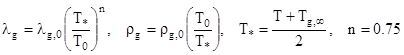где – критерии Рейнольдса, определяющие суммарную, вынужденную и естественную конвекции; Gr, Pr – критерии Грасгофа и Прандтля; V - относительная скорость частицы, м/с; _g – кинематическая вязкость газа, м² /с; g – ускорение свободного падения, м/с² ; а_g – температуропроводность газовой смеси, м² /с; - коэффициент теплопроводности газовой смеси, Вт/(м К); - коэффициент теплопроводности газовой смеси при , Вт/(м К); - коэффициент массообмена, м/с; - удельная теплоемкость газовой смеси, Дж/(кг К); - температура газовой смеси на бесконечном удалении от поверхности частицы, К; - коэффициент диффузии кислорода в газовой смеси, м² /с; - коэффициент теплообмена, Вт/м² К.

Зависимости относительных массовых концентраций кислорода (), диоксида углерода (), оксида углерода () и азота (), а так же скорость стефановского течения (), для , находятся из решений уравнений, в которых левые части представляют потоки масс газообразных компонент через произвольную поверхность радиуса r, а правые – скорости образования или исчезновения масс этих компонент в результате химических реакций

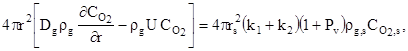
(10)

где – молярная масса угарного газа, кг/моль; - текущая скорость стефановского течения, м/с.

Предполагая, что коэффициенты диффузии компонент газовой смеси равны и, применяя условие, , из (10) получим уравнение неразрывности

, (11)

где Wc определяется формулой (6), - скорость стефановского течения на поверхности частицы, м/с.

Для решения (10) зададим граничные условия

и введем безразмерные координаты

, . (12)

Учитывая (8) и (9), получим, что безразмерная скорость стефановского течения на поверхности частицы

где - относительные массовые концентрации; j-1 для О₂ , 2 - СО₂ , 3 - СО, 4 - N₂ ; ― относительные массовые концентрации компонент газовой смеси на поверхности частицы и приведенной пленки.

Решение (10) и (11) представим в виде

или (13)

Скорость химического превращения углерода в газообразные компоненты может оказывать влияние на интенсивность теплообмена поверхности частицы с газом. Для определения плотности теплового потока, характеризующего теплообмен частицы с газом, воспользуемся предположением о квазистационарности поля температуры газовой фазы и частицы. В этом случае () тепловой поток через произвольную поверхность радиуса является постоянным и равен произведению плотности теплового потока на поверхность частицы.