Дипломная работа: Інформаційний синтез системи автоматичного розпізнавання бланків документів
Еталонний вектор xm - це математичне сподівання реалізацій класу
.
Він подається у вигляді детермінованого структурованого бінарного вектора 
, де хm,і - і-та координата вектора, яка приймає одиничне значення, якщо значення і-ї ОР знаходиться в нормованому полі допусків
, і нульове значення, якщо не знаходиться.
Основною задачею етапу навчання за МФСВ є розбиття простору ознак розпызнавання за поданою навчальною матрицею на області класів розпізнавання деяким оптимальним в інформаційному сенсі способом, який забезпечує на етапі екзамену прийняття рішень з достовірністю, наближеною до максимальної асимптотичної достовірності.
Параметром функціонування називається характеристика інформаційного забезпечення, яка прямо або непрямо впливає на функціональну ефективність системи. Такими параметрами можуть бути параметри навчання, перетворення образу, впливу середовища та інші, які безпосередньо впливають на асимптотичну достовірність.
Як критерій оптимізації процесу навчання системи прийняттю рішень в рамках МФСВ застосовується статистичний інформаційний КФЕ, який є природною мірою різноманітності (або схожості) класів розпізнавання і одночасно функціоналом асимптотичних точнісних характеристик СР. При цьому важливо, щоб параметри навчання були оптимальними в інформаційному розумінні, тобто забезпечували максимальну функціональну ефективність СР, яка визначається достовірністю прийняття рішень на екзамені.
Достовірність класифікатора залежить від геометричних параметрів роздільних гіперповерхонь класів розпізнавання.
У загальному випадку, коли класи розпізнавання перетинаються, розглянемо відносний коефіцієнт нечіткої компактності реалізації образу для класу
(2.1.1)
Процес навчання полягає в мінімізації цього виразу.
В МФСВ, який ґрунтується на допущенні гіпотези компактності (чіткої або нечіткої) реалізацій образу, як наближення ²точної² роздільної гіперповерхні для класу розглядається гіперсфера, центром якої є еталонний вектор 
, а радіусом 
- кодова відстань, яка у просторі Хеммінга визначається як
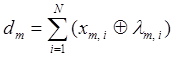(2.1.2)
де 
- і-та координата вектора
- i-тa координата деякого вектора lm, вершина якого знаходиться на роздільні гіперповерхні класу ; 
- операція складання за модулем два.
Оптимальною кодовою відстанню (радіусом) між вектором 
і контейнером 
називається екстремальне значення 
, яке визначає максимум інформаційного КФЕ 
, де {d} – послідовність збільшень радіуса контейнера 
.
Побудова оптимальної в інформаційному сенсі РГП у вигляді гіперсфери за МФСВ зводиться до оптимізації радіуса роздільної гіперсфери dm , яка відбувається за ітераційним алгоритмом
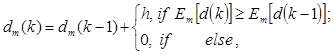(2.1.3)
де k - змінна числа збільшень радіуса РГП; h - крок збільшення.
Процедура закінчується при знаходженні екстремального значення критерію , де 
- множина радіусів концентрованих гіперсфер, центр яких визначається вершиною еталонного вектора 
- еталонний вектор найближчого (до
) класу
.
2.2 Математична модель системи розпізнавання рукописних символів
Категоріальну модель процесу навчання системи розпізнавання символів [19] при нечіткому розбитті за МФСВ подамо у вигляді діаграми відображень множин:
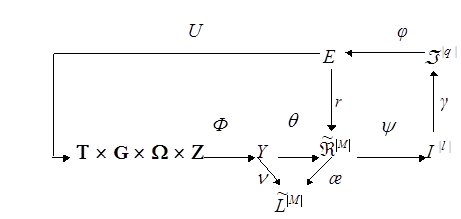(2.2.1)
де
- 
множина сигналів на вході СР
- 
множина моментів зчитування інформації з рецепторів;
- <