Дипломная работа: Исследование свойств магнитных жидкостей методом светорассеяния

где - составляет диаметр частицы вместе со стабилизующей оболочкой.

Из этой формулы можно оценить время, в течение которого частица магнетита в керосине при Т =300К сместится на расстояние, равное своему гидродинамическому диаметру:

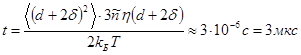
Кроме поступательного движения, частицы магнитной жидкости участвуют во вращательном броуновском движении, среднеквадратичное угловое смещение при котором описывается формулой

Коэффициент броуновской вращательной диффузии равен:

Можно оценить время, в течение которого частица магнетита в керосине при Т =300К повернется на , т.е. изменит свою ориентацию на 180˚:

Сам коэффициент вращательной диффузии для таких частиц равен

Статистические магнитные свойства МЖ

Коллоидные частицы ферромагнетика обладают постоянным по величине магнитным моментом. Внешнее магнитное поле упорядочивает направление магнитных моментов, а тепловое движение их разориентирует. Существуют два механизма дезориентации магнитных моментов коллоидных частиц. В твердой одноосной частице происходит тепловой «переброс» магнитного момента между двумя противоположными направлениями от легкого намагничивания кристалла. При малых размерах частиц энергия магнитной анизотропии KV становится сравнимой с тепловой энергией k_Б T . Тепловые флуктуации приводят к спонтанному изменению магнитного момента с одного направления на противоположное и к исчезновению среднего магнитного момента частицы, если время наблюдения больше характеристического процесса «переброса» магнитного момента. Неель в своих работах [46], [47] показал, что этот механизм специфичен для субдоменных частиц, а вероятность такого «переброса» пропорциональна , т.е. сильно зависит от размера частиц. Для времени релаксации , характеризующего процесс Нееля, Браун [39], [40] получил асимптотическую формулу

(),

справедливую при σ≥2 , где τ₀ связано с временем затухания ларморовой прецессии, зависит от σ и имеет величину порядка 10^-9 с. если время наблюдения t оказывается больше времени релаксации τ _N , то в результате тепловых флуктуаций магнитный момент успевает несколько раз изменить свое направление на противоположное и говорят, что частица является суперпарамагнитной [37]. В качестве критерия суперпарамагнетизма обычно выбирают равенство . С учетом того, что первая константа кристаллографической анизотропии магнетита равна Дж/м³ , критический объем частицы равен V_кр =4·10^-25 м³ , что как раз и соответствует частицам с диаметром d≈10 нм , что является средним оценочным параметром для жидкостей на основе магнетита. Критический размер свидетельствует о том, что коллоидные частицы магнетита могут проявлять как ферромагнитные, так и суперпарамагнитные свойства.

Второй механизм дезориентации магнитных моментов коллоидных частиц обусловлен броуновским (тепловым) вращением частиц относительно жидкой основы. При отсутствии магнитного дипольного взаимодействия между монодисперсными коллоидными частицами при помещении МЖ во внешнее магнитное поле в равновесном состоянии намагниченность жидкости зависит от объемной концентрации магнитного материала, величины магнитного момента частицы, приложенного поля и энергии разупорядочивающего теплового движения, и ее можно описать классическим законом Ланжевена, выведенным для намагниченности ансамбля молекул парамагнитного газа:

,

где φ_Т - объемная концентрация магнитного материала; - ланжевеновский аргумент; для сферических частиц ; Z(ξ) – функция Ланжевена.

Приведем асимптотические значения Ланжевена для слабых и сильных полей (т.е. для малых и больших значений аргумента ξ).

В слабых полях () при разложении функции Ланжевена в ряд Тейлора получаем:

Обычно пользуются значением и из него находят начальную магнитную восприимчивость

(ξ<<1)

где М_∞ =φ _m ·M _S – намагниченность насыщения жидкости в магнитном поле, напряженность которого Н→∞. М _S - намагниченность насыщения объемного магнетита.

В сильных полях () функция Ланжевена имеет вид:

и ; (ξ>>1)

В магнитной жидкости характерна полидисперсность частиц твердой фазы, чему свидетельствуют гистограммы распределения частиц по размерам, полученные с помощью электронного микроскопа УЭМВ – 100К. Среднее арифметическое выборки определялось по формуле

и оказалось равным 115 Å=11,5 нм для частиц Fe₃ O₄ ; 119Å=11,9 нм для частиц CoFe₂ O ₄ .

Кривые намагничивания, построенные по закону Ланжевена, показывают сильное влияние размера частиц магнетита на χ₀ и . (см. рис.) [28].

1.0

d =10 нм

0.5 d =7.5 нм

d =5нм

0 0.2 0.4 В (Тл)

Рис. 1

В основе гранулометрического метода определения размера малых магнитных частиц лежит сопоставление экспериментальных кривых намагничивания и зависимостью Ланжевена.

По зависимости М(Н^-1 ) для сильных полей можно найти d_∞ , а по начальному наклону кривой намагничивания в слабых полях можно найти диаметр частиц d₀ . Крупные частицы с относительно большими моментами легче ориентируются в слабых полях, чем мелкие, и именно они оказывают большее влияние на начальную магнитную восприимчивость. В области насыщения намагниченности в сильных полях ориентируются и особенно мелкие частицы с диаметром d_∞ . Средний размер, определяемый по измерениям намагниченности, лежит в пределах d_∞ < d< d₀ .

По данным зависимости намагниченности магнетитовой МЖ на основе керосина удается рассчитать эффективное значение магнитного момента m_эф , для которого сумма квадратов отклонений экспериментальных и расчетных значений минимальна, и по нему найти эффективный диаметр магнетита, который составил d_эф =11,7 нм , что находится в очень хорошем соответствии с данными электронной микроскопии d_ср =11,5 .

Нужно отметить , что результаты многолетних измерений намагниченности и определение по ним объемной концентрации частиц магнетита не совпадают с данными φ_Т , вычисленными по плотности, , а именно, объемная концентрация магнетита, вычисленная по магнитным измерениям, оказывается значительно меньше (примерно в 1,25 раза) концентрации, вычисленной по плотности.

В.Е. Фертман [28] указывает на несколько причин такого расхождения: