Дипломная работа: Исследование свойств магнитных жидкостей методом светорассеяния

2) в результате химического взаимодействия с адсорбированным ПАВ возможно образование немагнитного поверхностного слоя на дисперсных частицах магнита;

3) адсорбция на поверхности частиц молекул ПАВ и ионов, которые ориентируются так, что снижают реальный магнитный момент частиц магнетита.

Таким образом, мы приходим к выводу, что в МЖ, помещенной во внешнее магнитное поле, равновесная ориентация магнитных моментов коллоидных частиц может достигаться путем вращения частиц в окружающей жидкости (броуновский механизм) или путем движения магнитного момента относительно твердой частицы (неелевский механизм).

В зависимости от того, какой тип релаксации намагниченности реализуется в конкретной магнитной жидкости, пользуются или моделью жестких магнитных диполей, или моделью индуцированных диполей, и чаще всего приходится учитывать как броуновский, так и неелевский механизм релаксации.

Модели магнитных жидкостей

Исследования физических и химических свойств МЖ показали, что в одинаковых по внешним характеристикам МЖ (плотность, магнитная восприимчивость, вязкость и т.д.) могут наблюдаться различные по сложности явления и невозможно предположить единую модель магнитной жидкости, с позиций которой можно было бы объяснить все наблюдаемые явления.

Одночастичная модель МЖ

Простейшей моделью магнитного коллоида является одночастичная, согласно которой частицы магнитного материала представляют собой взвесь в несущей жидкости, сами частицы – сферы или эллипсоиды вращения, покрытые одним слоем ПАВ.

Для оценочных расчетов используются монодисперсные приближения сферических частиц со средним диаметром d_ср 10 нм , которые не взаимодействуют друг с другом, находясь в беспрерывном броуновском движении, энергия которого преобладает над энергией гравитационной и магнитной седиментации.

Коагуляция происходит под действием ван-дер-ваальсовых сил приближения между частицами при их сближении (так называемые дисперсионные силы, у которых энергия приближения с увеличением расстояния L между центрами частиц уменьшается пропорционально е^-6 ).

Гамакер получил выражение для энергии взаимодействия двух сфер одинакового диаметра d в виде:

где ; S – расстояние между поверхностями сфер; А – постоянная Гамакера, зависящая от диэлектрических свойств частиц и жидкой основы, которая определяет значение дисперсионных сил в данной системе.

Из этого выражения следует, что при соприкосновении сфер (S=0 ) энергия притяжения стремится к бесконечности и происходит объединение частиц.

В магнитном поле энергия притяжения двух сферических точечных диполей равна:

Агрегативная устойчивость коллоидных систем с магнитными частицами обеспечивается поверхностными адсорбционными слоями.

2

?? ???.2 ?????????? ?????????? ??? ???????, ???????? ?????????????? ??????. ???????? ??? ????? ???????? ?????? 1, ????????? ? ???????????? ??????? ?????????? ??? ?????????? ????????. ???????????????? ????????? ????? ???????? 2, ????????????? ? ?????? ?????????? ??????, ?????????? ?????????????? ????????? ????????.

1

2

Рис. 2

При сближении частиц адсорбционные слои деформируются и между ними возникает стерическое отталкивание, энергия которого по оценке Розенцвейга [23] при S≤2δ равна:

где N – поверхностная плотность адсорбционных молекул ПАВ, δ – толщина адсорбционного слоя. Из этого выражения следует, что существует максимальная энергия отталкивания для достаточно толстых адсорбционных слоев, равная:

Причин возникновения стерического отталкивания несколько. Во-первых, ему способствует ограниченность пространства, в котором происходит тепловое движение гибких концов молекул, что приводит к деформации молекул и возникновению буфера на каждой частице. Во-вторых, повышение концентрации длинноцепочечных молекул в зоне пересечения адсорбционных слоев вызывает осмотический эффект (увеличение давления в этой зоне).

Результат алгебраического суммирования энергий ван-дер-ваальсового притяжения, магнитного дипольного притяжения и стерического отталкивания монодисперсных магнетитовых частиц диаметром 10 нм приведен в справочном пособии В.Е. Фертмана [28]. Для δ=2 нм на кривой суммарной потенциальной энергии существует барьер порядка 25 кТ . Этого вполне достаточно, чтобы предотвратить коагуляцию частиц при броуновском столкновении. Кривая для нм показывает, что броуновское движение не приводит к дезагрегации, если расстояние между частицами меньше 3 нм. Тем не менее, наш опыт показывает, что в лабораторных условиях хранятся магнитные жидкости различных концентраций в течение 15-20 лет и сохраняют свои свойства неизменными.

Таким образом, одночастичная модель магнитного коллоида не только имеет право на существование, но и широко применяется, особенно для описания поведения частиц в сильно разбавленных магнитных жидкостях [35].

Модель цепочечных агрегатов в МЖ

Ясно, поскольку частицы в МЖ обладают собственными магнитными моментами, то это увеличивает вероятность образования ассоциатов частиц по сравнению с немагнитными частицами [31], [43] и др. Представления о цепочечных агрегатах используются при рассмотрении магнитооптических эффектов [5], [26], [44] и др.

Исследуя взаимодействие магнитных диполей в коллоидных частицах Джордан [43] рассмотрел силы, действующие между одинаковыми частицами такого типа.

Потенциальная энергия взаимодействия U двух магнитных диполей описывается следующими выражениями:

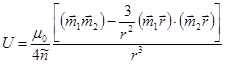
где ; и - соответственно магнитные моменты и радиус-векторы первой и второй магнитных частиц.

Для характеристики взаимодействия двух сферических магнитных частиц удобно ввести коэффициент связи при константе между ними:

;

Оценка коэффициента связи двух сферических частиц магнетита диаметром d =10нм, покрытых слоем ПАВ толщиной δ 2нм при Т =300К дает λ> 1. Следовательно, в такой жидкости могут иметь место процессы агрегирования.

Оценка энергии связи между магнитными частицами дает 25 кДж/моль, что сравнимо с энергией водородных связей (8-32 кДж/моль).

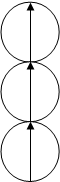
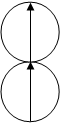
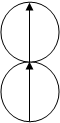
Джордан исследовал начальную стадию агрегирования, т.е. слипания нескольких магнитных частиц. Два случая объединения четырех коллоидных частиц с образованием либо двух пар, либо агрегата из трех частиц и одной отдельной частицы представлены на рис. 3.

а) б)

Рис.3