Дипломная работа: Коммутационно-фильтровое устройство радиолокатора непрерывного излучения с частотной манипуляцией и модуляцией
и максимально плоская
![]() .
.
Где Tn – полином Чебышева 1-го рода n-го порядка;
n – число звеньев фильтра;
![]()
![]() - частотная переменная;
- частотная переменная;
h – амплитудный множитель;
 ;
;
![]() ;
;
S – масштабный множитель;
![]() при
при ![]() ;
;
![]() ;
;
![]() - добротность (по уровню 3 дБ) фильтра с максимально плоской характеристикой.
- добротность (по уровню 3 дБ) фильтра с максимально плоской характеристикой.
Для чебышевского фильтра:
 ;
;
и для фильтра с максимально-плоской характеристикой:
 .
.
При этом
![]() ;
;
![]() ;
;
где bп и bз даны в дБ
и
 .
.
Второй этап синтеза заключается в определении коэффициента передачи Т11 по заданному в виде функции ![]() квадрату его модуля. Для этой цели необходимо найти корни уравнения
квадрату его модуля. Для этой цели необходимо найти корни уравнения
![]()
и представить функцию рабочего затухания в виде произведения двух комплексно-сопряженных множителей:
![]() .
.
Где h1 ,h2 ,…, hn – корни, расположенные в верхней полуплоскости комплексной переменной h;
h* 1 ,h* 2 ,…, h* n – сопряженные корни.
В качестве Т11 выбираем тот из сомножителей в (), корни которого лежат в верхней полуплоскости, т.е. соответствуют устойчивому полиному.
Третий этап синтеза состоит в определении сопротивления холостого хода Zxx фильтра по найденному значению Т11 . Если в заданной функции рабочего затухания ![]()
![]() полином
полином ![]() - нечетный, то фильтр будет симметричным; его сопротивление холостого хода следует определять по формуле:
- нечетный, то фильтр будет симметричным; его сопротивление холостого хода следует определять по формуле:
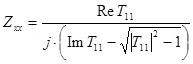 .
.
Если же ![]() - четный полином, то соответствующий фильтр антиметричный и сопротивление холостого хода вычисляется по формуле:
- четный полином, то соответствующий фильтр антиметричный и сопротивление холостого хода вычисляется по формуле:
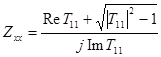 .
.
В последнем случае в схеме может понадобиться идеальный трансформатор, обеспечивающий ![]() ; это характерно для чебышевских фильтров с четным числом звеньев.
; это характерно для чебышевских фильтров с четным числом звеньев.
Четвертый этап синтеза заключающийся в определении числовых значений ветвей лестничной схемы. С этой целью найденное значение сопротивления холостого хода Zxx разлагается в цепную дробь:
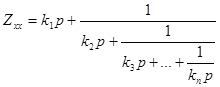 ;
;
и коэффициенты к1 , к2 ,… , кn отождествляются с элементами лестничной схемы. Если синтезируется полосно-пропускающий фильтр, то 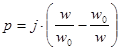 и к1 , к2 ,… , кn соответствуют добротностям параллельных и последовательных контуров в ветвях лестничной схемы.
и к1 , к2 ,… , кn соответствуют добротностям параллельных и последовательных контуров в ветвях лестничной схемы.
Приведенный выше метод в первоначальном своем виде неудобен при расчетах вследствие громоздкости и значительной вероятности ошибок.
Известны два способа преодоления этих трудностей. В первом способе выявляются общие закономерности в распределении добротностей контуров лестничной схемы; эти закономерности исследуются при разложении Zxx в цепную дробь и затем (по индукции) обобщаются. Наиболее простой закон распределения добротностей в фильтре с максимально плоской характеристикой:
![]() ,
,
где Qm – требуемая добротность m-го звена;
Qф – заданная добротность всего фильтра;
n – число звеньев фильра.
Второй способ преодоления расчетных трудностей заключается в полной каталогизации всех трудоемких процессов расчета.
Приведем пример расчета полосно-пропускающего фильтра (ППФ) по следующим произвольно заданным характеристикам:
![]() ГГц;
ГГц;