Дипломная работа: Математическая модель системы слежения РЛС
Содержание. 1
Введение. 3
1 Общая теория оптимального управления. 6
1.1 Допустимые управления. 6
1.2 Основные направления в теории оптимальных процессов. 11
1.2.1 Метод динамического программирования. 12
1.2.2 Принцип максимума. 13
1.3 Программное управление. 16
1.4 Постановка задачи и способы решения. 18
2 Система оптимального управления. 24
2.1 Математическое описание электромеханической системы.. 24
2.2 Идентификация авторегрессионно-регрессионной модели. 29
2.3 Формирование ограничений. 37
2.4 Формирование оптимальных траекторий. 42
2.5 Анализ решений. 50
2.6 Общая структура системы оптимального управления. 55
2.7 Полученные результаты.. 58
3 Практическая реализация. 63
3.1 Реализация оптимального управления в среде пакета matlab. 63
3.2 Выбор микроконтроллера. 64
4 Экономическое обоснование проекта. 66
4.1 Технико-экономическая характеристика. 66
4.2 Маркетинговая ориентация. 66
4.3 оценка научно-технической результативности и социальной эффективности НИР 68
4.4 Производственный план. 74
4.4.1 Расчёт затрат на разработку. 75
4.4.2 Затраты на создание опытного образца. 77
4.4.3 Затраты на эксплуатацию.. 79
4.4.4 Ценообразование. 79
Выводы.. 80
5 Безопасность и экологичность проекта. 81
5.1 Анализ опасных и вредных факторов. 82
5.2 Мероприятия по улучшению условий труда. 83
5.2.1 Помещения и их освещение. 83
5.2.2 Уровень шума и вибрация. 85
5.2.3 Параметры микроклимата. 86
5.2.4 Защита от электромагнитных и электростатических полей. 87
5.2.5 Электробезопасность. 90
5.2.6 Дисплейные терминалы и ПЭВМ в составе АРМ.. 91
5.2.7 Организация и оборудование рабочих мест с ВДТ и ПЭВМ.. 93
5.2.8 Требования к организации режима труда и отдыха при работе на АРМ.. 95
5.3 Устойчивость проекта к чрезвычайным ситуациям. 97
5.4 Экологичность проекта. 98
5.5 Выводы.. 99
Заключение. 100
Приложение. 101
Блок-схема файл-функции OPTIMUM_CONTR.. 101
Введение
Во многих областях техники и технологии приходится иметь дело со следующей задачей, которую можно трактовать как задачу «сопровождения цели». Причем, наблюдаемый процесс в некоторых случаях является детерминированным, т.е. полностью определенным, а в некоторых — не известным, но и в том и в другом случае в нем присутствует шум — случайная составляющая. Заданием для управляемого объекта служит движение другого объекта — задающего. Таким образом, задача слежения сводится к задаче перевода системы из начального состояния в наперед заданное состояние, которое определяется фазовым состоянием наблюдаемой системы.
В начальный момент времени t 0 объект находится в фазовом состоянии x 0 ; требуется выбрать такое управление u( t) , которое переведет объект в заранее заданное конечное фазовое состояние x 1 (отличное от x 0 ). При этом нередко бывает, что начальное состояние x 0 заранее неизвестно.
Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.
Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы сейчас очень распространены в технике, их изучением занимается теория автоматического управления.
В общем случае на вход регулятора подаются фазовые координаты объекта. Регулятор конструируется так, что его выходная величина u , поданная на вход объекта, нужным образом управляет работой объекта (т. е., например, возвращает объект в рабочее состояние, если он почему-либо вышел из этого состояния).
Обычно требуется, чтобы переходный процесс (т. е. процесс перехода из начального фазового состояния x 0 в предписанное конечное состояние x 1 ) был в определенном смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. п. Такой «наилучший» переходный процесс называется оптимальным процессом.
Разумеется, желательно, чтобы регулятор не просто возвращал объект в рабочее состояние, а делал это наилучшим образом, например, в смысле быстродействия (т.е. возвращал объект в рабочее состояние за кратчайшее время). В связи с этим в теории автоматического управления рассматриваются весьма различные (по устройству и степени сложности) регуляторы. Рассмотрение регуляторов, которые применялись на практике и изучались в руководствах по автоматическому регулированию до возникновения теории оптимальных процессов, приводит к выводу, что уменьшение времени переходного процесса связано с усложнением конструкции регулятора; поэтому, усложняя конструкцию регулятора, можно лишь приближаться к «идеальному», «оптимальному» регулятору, который во всех случаях осуществляет переходный процесс за кратчайшее время.
Одной из важных заслуг теории оптимальных процессов является установление существования оптимальных регуляторов и создание математического аппарата, позволяющего рассчитывать такие регуляторы. Оптимальные регуляторы существенно отличаются от тех, которые до сих пор изучались в теории автоматического управления.
На данном уровне развития техники и технологии для такого рода управления в большинстве случаев используются стандартные регуляторы (например, ПИД-регуляторы). Во многих случаях их применение может быть оправдано и их работа удовлетворяет поставленным целям управления, но существуют ситуации, в которых применение таких регуляторов не дает необходимого результата. Использование ПИД-регуляторов может оказаться нецелесообразным в случае ограничений на управление. В такой ситуации, система в целом оказывается существенно нелинейной и классические приемы управления в этом случае не приемлемы.
В данной работе рассматривается система, состоящая из двух электроприводов, один из которых является ведущим, а другой — ведомым. Ведомый двигатель должен двигаться синхронно с ведущим. Система должна отрабатывать заданную траекторию с необходимой точностью и максимальным быстродействием.
1 Общая теория оптимального управления
1.1 Допустимые управления
Наиболее перспективным решением экстремальных задач является их решение на основе теории принципа максимума Понтрягина. В данной работе ставилась задача оптимизации по времени, для чего и были использованы методы оптимального управления, предложенные Л.С. Понтрягиным, В.Г. Болтянским, Р.В. Гамкрелидзе. [1]
Задача оптимального быстродействия заключается в отыскании такого управления u( t) , для которого фазовая траектория x( t) проходит через точку x1 и переход из х0 в х1 осуществляется за кратчайшее время. Такое управление u( t) называется оптимальным управлением (в смысле быстродействия) ; точно так же соответствующую траекторию x( t) , по которой фазовая точка за кратчайшее время переходит из состояния x0 в состояние x1 называется оптимальной траекторией .
Обычно управляющие параметры u1 ,..., ur не могут принимать совершенно произвольные значения, а подчинены некоторым ограничениям. Это обусловлено техническими характеристиками реальных объектов управления, а также конструкцией регулирующих устройств.
Например, для двигателя постоянного тока (ДПТ), одним из управляющих параметров служит напряжение якоря; однако именно в силу конструктивных особенностей ДПТ этот параметр подчинен ограничениям указанного типа. Так, значение этого параметра не может принимать сколь угодно большое значение.
Для объекта, содержащего r управляющих параметров u1 , u2 , ..., ur , в приложениях часто встречается случай, когда эти параметры могут произвольно меняться в следующих пределах:
![]()
Т. е. каждая из величин u1 , u2 , ..., ur представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задается неравенствами
![]() (1.1)
(1.1)
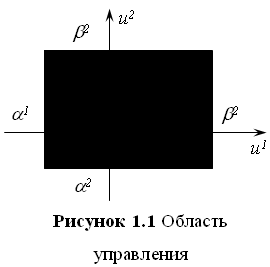
Заметим, что при r = 2 точки ![]() , координаты которых подчинены неравенствам (1.1), заполняют прямоугольник (рисунок 1.1); при r = 3 неравенства (1.1) определяют в пространстве переменных u1 , u2 , u3 прямоугольный параллелепипед.
, координаты которых подчинены неравенствам (1.1), заполняют прямоугольник (рисунок 1.1); при r = 3 неравенства (1.1) определяют в пространстве переменных u1 , u2 , u3 прямоугольный параллелепипед.
В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано в пространстве переменных u1 , ..., ur некоторое множество U и управляющие параметры u1 , u2 , ..., ur должны в каждый момент времени принимать лишь такие значения, чтобы точка ![]() принадлежала множеству U . Т. е. разрешается рассматривать лишь такие управления u( t) , что
принадлежала множеству U . Т. е. разрешается рассматривать лишь такие управления u( t) , что ![]() для любого t . Множество U называется областью управления .
для любого t . Множество U называется областью управления .
--> ЧИТАТЬ ПОЛНОСТЬЮ <--