Дипломная работа: Механизмы имплантации в металлы и сплавы ионов азота с энергией 1-10 кэВ
Для нахождения вышеуказанных параметров рассмотрим процесс столкновений частиц на основе классической механики. Тогда с углом рассеяния сталкивающихся частиц можно связать прицельный параметр p и классическую траекторию в процессе столкновения. Уравнения, описывающие траектории взаимодействующих частиц, значительно упрощаются, если рассматривать движение в системе центра масс (СЦМ). Рисунок 2.5 иллюстрирует положение и угловые координаты частиц при максимальном их сближении в лабораторной системе координат (ЛСК). Одна из частиц (M1 ) до столкновения двигалась со скоростью v , а другая (M2 ) – покоилась. Углы отклонения частиц после столкновения в ЛСК q1 и q2 выражаются через угол j формулами [22]:
, 
, (2.6)
где α – угол отклонения иона в СЦМ при столкновении, рад .
Абсолютные величины скоростей частиц после столкновения 
и 
могут быть выражены через угол α формулами [22]:
, 
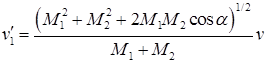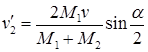. (2.7)
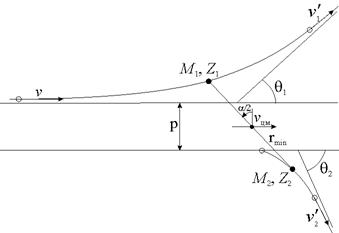
Рисунок 2.5 – Схема столкновения двух частиц в ЛСК.
- скорость иона до и после столкновения соответственно; 
- скорость атома после столкновения; 
- скорость центра масс; θ1 , θ2 – углы отклонения в ЛСК после столкновения иона и атома соответственно; α - угол отклонения иона в СЦМ; p - прицельный параметр; r min - минимальное расстояние сближения частиц.
Тогда упругие потери энергии Tn ионом при столкновении с атомом подложки в ЛСК рассчитываются согласно (2.7) по формуле:
, (2.8)
где E – энергия иона до столкновения; параметр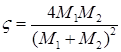 
Дж , определяет максимально возможную энергию, передаваемую при лобовом столкновении (когда частицы сближаются и удаляются по одной оси):
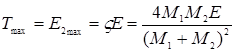. (2.9)
Угол рассеяния α налетающей заряженной частицы в центральном силовом поле c потенциальной энергией U (r ) наиболее удобно решать исходя из законов сохранения энергии 
и момента импульса 
:
, (2.10)
. (2.11)
где r – радиус-вектор иона, м ; p - прицельный параметр, м (расстояние, на котором ион прошёл бы от атома в отсутствие силового поля);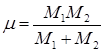
- приведенная масса, кг ; 
и 
- радиальная и поперечная составляющие скорости иона соответственно.
Подставим величину 
из (2.11) в (2.10):
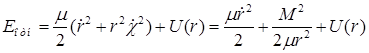. (2.12)
Отсюда
