Дипломная работа: Моделирование и методы измерения параметров радиокомпонентов электронных схем

Структурная схема рис. 1.1, по существу, отвечает классификации ЭБ РЭС, ориентированной на применение РК в САПР.

1.2. Связь двухполюсных и многополюсных радиокомпонентов

Разделение РК на ДП и МП достаточно условное. Так, любой ДП в зависимости от способа включения в электрическую схему можно рассматривать как собственно ДП или как МП, а именно четырёхполюсник рис. 1.2.

а)б)

Рис. 1.2. - Варианты включения ДП: а) как собственно ДП;

б) как четырёхполюсник; у - его полная проводимость.

0,1,2 - узлы подключения к схеме.

С другой стороны любой МП моно включить как ДП, например соединяя с общей шиной все полюса МП, кроме одного.

При проектирование РК и идентификации его параметров необходимо учитывать область действия физических законов связанных с его функционированием. Особое внимание необходимо уделять электрофизическим законам которые определяют основные электрические параметры РК. В каждом конкретном случае доминирует одно из электрофизических явлений, но также проявляется влияние и других паразитных.

Количество МП можно считать безграничным так как МП проектируется на основе ДП, а каждому реальному МП отвечает определённый способ соединения составляющих его ДП.

1.3. Модели радиокомпонентов

1.3.1.Общие положения

Под моделью РК будем понимать любое математическое описание, отражающее с требуемой точностью его поведение в реальных условиях.

Если РК является элементом электронной схемы, то его моделью будем называть математическое описание связей между токами и напряжениями, возникающими между его полюсами в статическом и динамическом режимах работы. В частности моделями могут быть уравнения вольт - амперных характеристик (ВАХ), дифференциальные уравнения переходных процессов, частотные характеристики и т.п. [4,5].

Математическую модель РК можно рассматривать как некоторый оператор, ставящий в соответствие системе внутренних параметров , ... , совокупность связанных между собой внешних параметров ... , . Вид функциональной связи зависит от принципа действия РК, а содержание"внешних" и "внутренних" параметров РК определяет его физическая сущность и способ использования.

Так для моделей РК внешними параметрами являются токи и напряжения, так как преобладающим методом расчёта электрических схем является расчёт по токам и напряжениям [5].

Внутренними параметрами модели РК могут быть его электрические, электрофизические или конструктивно-технологические параметры.

Электрическими будем считать параметры, определяемые только при электрических измерениях (коэффициенты усиления, крутизна, входное и выходное сопротивления и т.п.). В некоторых случаях это параметры "чёрного ящика", которым трудно придать физический смысл. Электрические параметры, как правило, являются функциями электрофизических и конструктивно—технологических параметров, которые можно считать первичными параметрами, а электрические - вторичными.

При расчёте интегральных схем (ИС) важное значение имеет учёт первичных параметров с точки зрения оптимизации процесса изготовления ИС.

При расчётах электронных схем, спроектированных на основе готовых конструктивно завершённых компонентов, что характерно для предприятий сборщиковрадиоэлектронных средств (РЭС), достаточно владеть

информацией только о внешних параметрах РК. По сути дела внешние параметры РК при этом выполняют функцию внутренних параметров проектируемого изделия.

1.3.2.Классификация моделей радиокомпонентов

Достаточно убедительная классификация моделей РК, приведённая в [5], отражена на структурной схеме рис. 1.3.

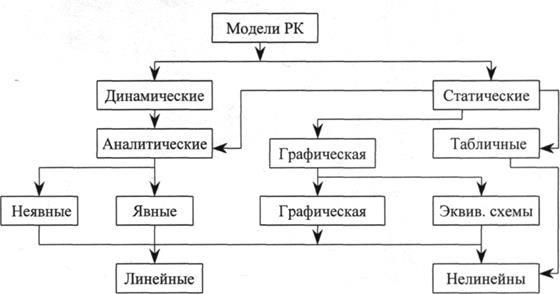
Рис. 1.3. - Классификация моделей РК

Статические модели отражают только связь между постоянными токами и напряжениями, тогда как динамические учитывают частотные или временные зависимости параметров РК, возникающими из-за влияния внутренних индуктивностей и ёмкостей РК.

По способу представления модели могут быть заданы аналитически, графически или таблично. Отсюда следуют понятия аналитических, графических и табличных моделей. Такое разделение нужно считать условным. На практике, как правило, широко используют комплексные модели РК. Например, на графических моделях типа эквивалентных схем для описания нелинейных элементов широко используют аналитические зависимости, а обработка данных табличных моделей производится математическими методами по специально разработанных алгоритмам.

Аналитические статические модели РК представляют обычно в виде явных зависимостей токов и напряжений, выраженных в виде уравнений ВАХ.

Динамические модели удобно представлять в неявном виде в форме дифференциальных уравнений [5].

Графические модели могут быть представлены в двух видах: в форме графиков функциональной связи токов и напряжений, в форме эквивалентныхсхем. Эквивалентные схемы наглядны, но требуют дополнительного анализа для получения значений токов и напряжений, что существенно усложняет общуюструктуру схемы анализируемого устройства.

Графическую статическую модель можно представить в форме графиков ВАХ или в форме статической эквивалентной схемы. Графики ВАХ не позволяют их непосредственное использование, так как для их ввода в ЭВМ необходимы преобразования в цифровую форму. С другой стороны, эквивалентная схема требует дополнительного описания в виде аналитических зависимостей между токами и напряжениями нелинейных элементов, входящих в состав этой схемы. Эквивалентная схема удобна для анализа функционирования РК, моделируемого этой схемой, а для расчёта РЭС более удобна соответствующая ей аналитическая макромодель, в которую включено математическое описание тех её элементов, параметры которых зависят от статического режима [5].

Табличные модели представляют собой таблицы соответствующих графиков ВАХ. Полученные экспериментальным путём, по которым рассчитывают соответствующие режимы РК. Для получения таких таблиц целесообразно использовать теорию методов планирования эксперимента [5].

На практике любую из рассматриваемых моделей оформляют в виде библиотечной подпрограммы, задав алгоритм вычисления требуемых для анализа параметров РЭС по данным аналитических или графических моделей.

Современное развитие ЭВМ и измерительной техники позволяет среди аналитических и графических моделей выделить класс алгоритмических моделей [5], которые характерны тем, что вследствие сложности связей между токами и напряжениями рассчитывать их можно только численными методами, задав алгоритм, метод вычислений. По существу это цифровые модели, которые реализуются в виде подпрограмм, обрабатывающих экспериментальные данные на этапе подготовки данных или во время расчёта РЭС.