Дипломная работа: Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

Постановка задачи о распределении концентрации вредных примесей при закачке растворов в глубоко залегающие пористые пласты основана на законе сохранения массы входящих в состав примесей. Для загрязнителя, находящегося в скелете пласта, справедливо уравнение неразрывности

(1.3.1)

где – диффузионный поток вещества в скелете, – соответственно плотность и коэффициент диффузии радиоактивного вещества в скелете, m – пористость скелета, – функция массообмена между скелетом и жидкостью, показывающая изменение плотности вещества в скелете за счёт диффузии молекул примеси из жидкости в скелет, – функция источников концентрации, определяющая потери загрязнителя за счёт радиоактивного распада.

Для загрязнителя, находящегося в жидкости, уравнение неразрывности принимает вид

,

(1.3.2)

где – диффузионный поток радиоактивного вещества в жидкости, текущей в пласте, – соответственно плотность и коэффициент диффузии радиоактивного вещества в жидкости. Будем считать, что процесс перехода молекул примеси из жидкости в скелет и её переход из скелета в жидкость определяется соотношением химических потенциалов . При этом, из закона сохранения следует, что потоки вещества из жидкости в скелет и обратно равны, но противоположны по знаку. Это приводит к появлению в правых частях уравнений одной и той же функции , но с противоположным знаком. Полагая далее пористость m постоянной, и складывая уравнения (1.3.1) и (1.3.2), получим

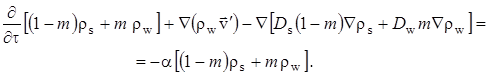(1.3.3)

Равновесные концентрации примеси в скелете и в жидкости связаны между собой соотношением (изотерма сорбции), где – некоторая функция концентрации примеси в жидкости.

Будем считать, что зависимость концентрации примеси в скелете от концентрации её в жидкости линейна (изотерма Генри), что является хорошим приближением при сравнительно небольших концентрациях мигранта

,

(1.3.4)

где – коэффициент распределения загрязнителя между носителем и скелетом.

Тогда последнее уравнение принимает вид

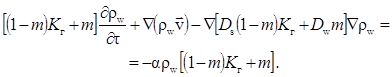(1.3.5)

Учитывая, что для несжимаемой жидкости , а следовательно, , из последнего уравнения получим

.

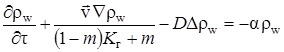(1.3.6)

Здесь введено обозначение

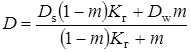(1.3.7)

– эффективный коэффициент диффузии в пласте. Из (1.3.6) следует, что в уравнении, описывающем миграцию загрязнителя, необходимо учитывать конвективный перенос загрязнителя, “осложнённый” наличием пористости в скелете и протекающими массообменными процессами между загрязнителем и скелетом. Уравнение (1.3.6) позволяет определить скорость конвективного переноса примесей в пористой среде по аналогии со скоростью конвективного переноса тепла и скоростью фильтрации

.

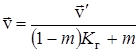(1.3.8)

Скорость конвективного переноса примеси определяет положение фронта загрязнения R _d подобно тому, как скорость фильтрации определяет положение фронта закачиваемой жидкости R _w . При этом положение фронта закачиваемой жидкости определяется из баланса массы закачиваемой жидкости. В случае закачки с постоянной скоростью через скважину радиуса r ₀ выражение для R _w имеет вид

.

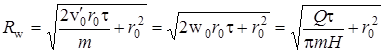(1.3.9)

Соответствующие радиусы зоны загрязнения и термических возмущений определяются в пунктах 2.1 и 3.1.

1.4. Задача теплопереноса

1.4.1. Математическая постановка задачи теплопереноса и её обезразмеривание

Рассмотрим задачу о распространении радиоактивных примесей в пористом глубоко залегающем пласте, в который закачивается жидкость с растворёнными радиоактивными веществами. Такая задача является фундаментальной для подземного захоронения радиоактивных отходов и отходов химических производств.

Одним из способов прогнозирования динамики поведения радиоактивных и химических примесей в глубокозалегающих пластах, является исследование их температурных полей. Современные приборы и методики измерения температуры позволяют проводить оперативные измерения с точностью, превосходящей тысячные доли градуса. Температурные измерения в таких условиях можно использовать для контроля продвижения радиоактивной зоны.

Соответствующие температурные аномалии возникают как за счет отличия температуры закачиваемой жидкости от естественной температуры пластов, так и за счет энергии, выделяющейся при распаде радиоактивных веществ.

В результате одного акта радиоактивного распада выделяется энергия ~ 1 МэВ. Согласно действующим в России Нормам радиационной безопасности и санитарным правилам высокоактивными жидкими радиоактивными отходами (РАО) признаются отходы, активность которых > 1 Ки/л. Следовательно, для высокоактивных отходов выделяемая мощность оказывается порядка ~ ~ 5 Вт/м³ . Причём, для средне- и долгоживущих нуклидов эта мощность мало меняется на протяжении лет и даже десятилетий. Выделяемая энергия является весьма существенной и приводит к значительному изменению температурного поля.

На рис. 1.1 представлена геометрия задачи в цилиндрической системе координат, ось z которой совпадает с осью скважины. Среда представлена тремя областями с плоскими границами раздела z = ±h . Закачка примесей в область ‑h < z < h производится из скважины радиуса r ₀ ; покрывающий (кровля) и подстилающий (подошва) пласты считаются непроницаемыми; средняя область толщины 2h является пористой; все пласты считаются однородными и анизотропными по теплофизическим свойствам.

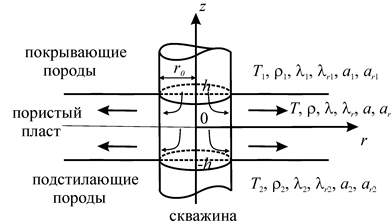
Рис. 1.1. Геометрия задачи теплопереноса

Через скважину малого (по сравнению с расстоянием до точки наблюдения) радиуса в горизонтальный бесконечный пласт толщиной закачивается вода с радиоактивным загрязнителем.

В поступающей в пласт жидкости (при ) поддерживаются постоянная температура и концентрация примеси . В общем случае температура и концентрация загрязнителя в пласте изменяются за счёт конвективного переноса вдоль направления , радиальной теплопроводности и диффузии вдоль , теплопроводности и диффузии вдоль , за счёт наличия тепловых источников и источников концентрации (в нашем случае такими источниками является радиоактивный распад загрязнителя).

В окружающих средах имеет место теплопроводность и диффузия вдоль и радиальная теплопроводность и диффузия вдоль . В пласте концентрация примеси , температура – , коэффициент диффузии вдоль равен , коэффициент теплопроводности – , коэффициент радиальной диффузии – , коэффициент радиальной теплопроводности – , в покрывающих пласт породах соответственно – , , , , , , в подстилающих породах – , ,, , , . Кроме того, постулируются условия равенства температур и концентраций, а также плотностей тепловых и диффузионных потоков на границах соприкосновения, накладываются начальные и граничные условия. В начальный момент времени везде и в бесконечно удалённых точках всегда концентрации примеси в пласте и в окружающих средах равны нулю.

Математическая постановка задачи теплопереноса для всех областей, таким образом, включает уравнение теплопроводности с учётом радиоактивного распада в покрывающем

(1.4.1)

и подстилающем

(1.4.2)

пластах, а также уравнение конвективного переноса с учётом радиоактивного распада в пористом пласте

(1.4.3)

Сомножитель при во втором слагаемом ?