Дипломная работа: Особенности термического режима рек

где n ₀ – общая облачность, в долях единицы, b ₁ = 0,38, а ₁ – коэффициент, зависящий от широты местности (Винников, Проскуряков, 1988).

Эффективное излучение воды I _эф это разница между собственным излучением водной поверхности I _с и встречным излучением атмосферы I _а :

I _эф = I _c – I _a . (2.12)

Величина I _с определяется с использованием закона Стефана-Больцмана для абсолютно черного тела:

I _а.ч.т. = σТ ⁴ , (2.13)

где постоянная σ = 5,7×10^-8 Вт/(м² ×К⁴ ), Т – абсолютная температура воды, К (Хромов, Петросянц, 2001). Так как вода не абсолютно черное тело, то для расчета ее собственного излучения правую часть выражения (2.13) умножают на поправочный коэффициент «серости» тела δ_в , который для воды меняется от 0,95 до 0,963 при изменении ее температуры θ в диапазоне 0100⁰ С (Винников, Проскуряков, 1988).

Теплообмен между поверхностью воды и воздухом осуществляется (при отсутствии льда) за счет механизма конвективной теплопередачи и определяется по «закону» Ньютона (Алексеевский, 2006):

q _k = -α (θ – θ_в ), (2.14)

где q_k – поток тепла через единицу площади водной поверхности, θ – температура воды, θ_в – температура воздуха, α – коэффициент теплоотдачи. Этот коэффициент зависит от ряда факторов, влияющих на интенсивность теплоотдачи:

α = 2,65 [1 + 0,8w + f (Δθ)], (2.15)

где w – скорость ветра на высоте 2 метра, м/с; f (Δθ) – функция, зависящая от разности температур θ-θ_B (Винников, Проскуряков, 1988). Если θ-θ_B > 0, то dq _k < 0 и водная масса охлаждается. Если θ-θ_B < 0, то dq _k > 0 и вода нагревается в соответствии с уравнением (2.2).

Тепло, поступающее с атмосферными осадками Θ_x , определяется по формуле:

Θ_x = C ρθ_ос Sx , (2.16)

где С – теплоемкость воды, Дж/(кг×⁰ С); ρ – плотность воды, кг/м³ ; S – площадь зеркала воды, км² ; x – слой осадков, мм; θ_ос – средняя температура атмосферной влаги.

Влияние поступления тепла с атмосферными осадками на температуру речной воды выражается повышением или понижением температуры воды в зависимости от знака разности температур речной воды и атмосферных осадков. Если θ_ос <θ, то происходит охлаждение речной воды. Если θ_ос >θ, то происходит увеличение удельного теплосодержания водной массы q _у (Дж/м³ ). Если рассматривать теплоту как консервативную примесь, то

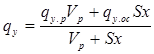, (2.17)

где q _{y . p} – удельное теплосодержание воды реки до поступления осадков, W_p – объем воды на данном участке реки, x – количество осадков, мм, S – площадь водной поверхности, Q_{y . oc} – удельное теплосодержание осадков.

Затраты или поступление теплоты в водную массу в случае испарения или конденсации водяного пара:

Θ_конд = Θ_исп =L _и m = L _и E ρ, (2.18)

где m – масса испаряемой или конденсируемой влаги; E – слой испарившейся (сконденсировавшейся) воды за единицу времени, м/ч; ρ – плотность воды, кг/м³ ; L _и – удельная теплота испарения, Вт×ч/кг. Последняя величина зависит от температуры испаряющей поверхности θ_п (Алексеевский, 2006):

L _и = (25 – 0,024θ_п )× 10⁵ , (2.19)

где 25×10⁵ Дж – удельная теплота испарения при температуре поверхности воды 0⁰ С. Количество испарившейся воды может быть рассчитано, например, по формуле Б.Д. Зайкова (Винников, Проскуряков, 1988). Тогда, с учетом (2.18), количество теплоты, теряемое водой при испарении, равно:

Q _и = 4,1 (1 + 0,72w ₂ ) (e ₀ -e ₂ ), (2.20)

где w ₂ – скорость ветра на высоте 2 м над поверхностью воды, e ₀ – давление насыщенного водяного пара в воздухе при температуре испаряющей поверхности, e ₂ – парциальное давление водяного пара на высоте 2 м.