2. При максимальном коэффициенте передачи неравномерность АЧХ не должна быть более ± 0.5 Дб .

Используя эти критерии применительно к наиболее часто используемым схемам усилителей с МКЦ [2 – 35], с помощью программы OPTIMAMP, был проведен их сравнительный анализ. Исследованные схемы изображены на рисунках 2.7 – 2.22 [2–35].

Рисунок 2.7 – Четырехполюсная реактивная КЦ третьего порядка.

Рисунок 2.8 – Четырехполюсная диссипативная КЦ второго порядка.

Рисунок 2.9 – Двухполюсная диссипативная КЦ первого порядка.

Рисунок 2.10 – Двухполюсная диссипативная КЦ второго порядка.

Рисунок 2.11 – Двухполюсная диссипативная КЦ третьего порядка.

Рисунок 2.12 – Четырехполюсная диссипативная КЦ третьего порядка.

Рисунок 2.13 – Двухполюсная диссипативная КЦ второго порядка.

Рисунок 2.14 – Четырехполюсная реактивная КЦ третьего порядка.

Рисунок 2.15 – Двухполюсная реактивная КЦ первого порядка.

Рисунок 2.16 – Четырехполюсная диссипативная КЦ третьего порядка.

Рисунок 2.17 – Четырехполюсная диссипативная КЦ третьего порядка.

Рисунок 2.18 – Двухполюсная реактивная КЦ второго порядка.

Рисунок 2.19 – Четырехполюсная диссипативная КЦ третьего порядка.

Рисунок 2.20 – Четырехполюсная диссипативная КЦ второго порядка.

Рисунок 2.21 – Четырехполюсная диссипативная КЦ второго порядка.

Результаты анализа представлены в таблице 2.2. Как видно из таблицы максимальный коэффициент усиления при заданной неравномерности АЧХ ±0.5Дб имеют схемы 2.7, 2.14 и 2.16. На рисунках 2.23. и 2.24 приведены АЧХ эти усилителей на транзисторах 3П602А и КП907Б соответственно.

Таблица 2.2 – Сравнительный анализ схем усилителей с МКЦ.

Номер схемы	Коэффициент передачи для транзистора 3П602А в диапазоне частот 100-2000 МГц	Коэффициент передачи для транзистора КП907Б в диапазоне частот 10-200 МГц
2.7	2.34	1.65
2.8	1.44	0.96
2.9	1.41	0.92
2.10	1.4	0.92
2.11	1.39	0.9
2.12	1.33	0.92
2.13	1.62	0.51
2.14	2.2	1.456
2.15	1.01	–––––
2.16	2.16	1.11
2.17	1.74	1.16
2.18	1.78	1.16
2.19	1.62	0.49
2.20	0.92	–––––
2.21	1.4	0.92

––––– - 2.7, ––––– -2.14, ––––– - 2.16.

Рисунок 2.23 – АЧХ усилителей на транзисторе 3П602А.

––––– - 2.7, ––––– - 2.14, ––––– - 2.16.

Рисунок 2.24 – АЧХ усилителей на транзисторе КП907Б.

Как видно из рисунков 2.23 и 2.24 максимальный коэффициент усиления имеет схема изображенная на рисунке 2.7. Однако при подробном рассмотрении этой схемы выявляются следующие особенности. Емкость Свых транзистора включается последовательно с С1 . Так как при исследовании первый транзистор заменялся идеальным генератором напряжения, то влияние Свых учтено не было. Если учитывать это влияние, то коэффициент передачи данной корректирующей приблизиться к МКЦ рисунка 2.14. В МКЦ рисунка 2.14 емкость Свых включена параллельно С1 . Поэтому её влияние может быть скомпенсировано уменьшением емкости C 1 на величину Свых. К тому же методика расчета усилителя с МКЦ рисунка 2.7 приведена в работе [30].

Исходя из всего вышесказанного, было принято решение о разработке методики расчета усилителя с МКЦ на мощном полевом транзисторе схемы изображенной на рисунке 2.14.

3 Расчет МКЦ по результатам сравнительного анализа

3.1 Общие положения методики расчета МКЦ

Для разработки методики расчета СУМ с выбранной МКЦ воспользуемся методом параметрического синтеза, описанного в [44]. Метод заключается в следующем. Согласно [37,43,44], коэффициент передачи усилительного каскада с МКЦ, в символьном виде, может быть описан дробно-рациональной функцией комплексного переменного:

, (3.1)

где ;

- нормированная частота;

- текущая круговая частота;

- верхняя круговая частота полосы пропускания широкополосного усилителя мощности, либо центральная круговая частота полосового усилителя;

- коэффициент передачи каскада на средних частотах;

– коэффициенты, являющиеся функциями параметров МКЦ и элементов аппроксимации входного импеданса транзистора усилительного каскада, нормированных относительно и сопротивления источника сигнала .

Зная коэффициенты всегда можно рассчитать нормированные значения элементов МКЦ и составить таблицы нормированных значений элементов, соответствующих заданному наклону АЧХ. В этом случае, проектирование усилительного каскада сводится к расчету истинных значений элементов МКЦ, соответствующих заданным и .

Для расчета коэффициентов в [44] предложено воспользоваться методом оптимального синтеза теории фильтров [43].

В соответствии с указанным методом представим нормированное значение квадрата модуля передаточной характеристики (3.1) в виде:

, (3.2)

где .

Для расчета коэффициентов составим систему линейных неравенств:

(3.3)

где - дискретное множество конечного числа точек в заданной нормированной области частот; - требуемая зависимость на множестве ; - допустимое уклонение от ; - малая константа.

Первое неравенство в (3.3) определяет величину допустимого уклонения АЧХ каскада от требуемой формы. Второе и третье неравенства определяют условия физической реализуемости рассчитываемой МКЦ. Учитывая, что полиномы числителя и знаменателя функции положительны, модульные неравенства можно заменить простыми и записать задачу в следующем виде:

(3.4)

Неравенства (3.4) являются стандартной задачей линейного программирования. В отличие от теории фильтров, где данная задача решается при условии минимизации функции цели: , неравенства (3.4) следует решать при условии максимизации функции цели: , что соответствует достижению максимального коэффициента усиления рассчитываемого каскада. Решение неравенств (3.4) позволяет получить векторы коэффициентов, соответствующие заданным и .

По известным коэффициентам функции (3.2), коэффициенты функции (3.1) определяются с помощью следующего алгоритма [43]:

1. В функции (3.2) осуществляется замена переменной , и вычисляются нули полиномов числителя и знаменателя.

2. Каждый из полиномов числителя и знаменателя представляется в виде произведения двух полиномов, один из которых должен быть полиномом Гурвица.

3. Отношение полиномов Гурвица числителя и знаменателя является искомой функцией (3.1).

Многократное решение системы линейных неравенств (3.4) для различных и , расчет векторов коэффициентов и вычисление нормированных значений элементов рассматриваемой МКЦ позволяют осуществить синтез таблиц нормированных значений элементов МКЦ, по которым ведется проектирование усилителей.

3.2 Вывод аналитического выражения для описания коэффициента передачи каскада с МКЦ

Воспользовавшись вышеописанным методом расчета, произведем расчет схемы, представленной на рисунке 2.14. Для вывода аналитического выражения коэффициента передачи каскада с МКЦ в схеме 2.6 заменим полевой транзистор его однонаправленной моделью [40]. Полученная схема представлена на рисунке 3.1.

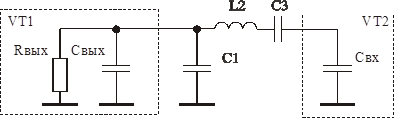
Рисунок 3.1. – Схема каскада с МКЦ.