Дипломная работа: Разработка подсистемы морфологического анализа информационной системы

1) Поиск слова в словаре.

2) В случае, если слово не найдено, производится попытка найти в этом слове ошибку.

На первом этапе используется словарь, состоящий из основ слов с префиксами и соответствующих этой основе окончаний. Поиск производится перебором. Одной словоформе может соответствовать много морфологических интерпретаций. Например, у словоформы стали две интерпретации:

· {СТАЛЬ, C, «но», («жр, ед, рд», «жр, ед, дт», «жр, мн, им», «жр, мн, вн»)};

· {СТАТЬ, Г, «нп, св», («мн, дст, прш»)}.

Второй этап выполняется, если слово не было найдено в словаре. В таком случае подразумевается, что слово содержит ошибку, и подсистема пытается определить, в каком месте слова допущена ошибка.

Если и на втором этапе не удалось найти словоформу, то считается, что слова нет в словаре.

2.4 Алгоритм поиска слова в словаре

При выборе структуры словаря были рассмотрены модели русского языка, а так же учитывались рекомендации. Потому в качестве основы был выбран словарь. Он содержит примерно 124000 корней, что позволяет покрыть достаточно большую часть русского языка (около 300000 слов).

Общим подходом словарь похож на корневую часть словаря и представляет собой текстовый файл в особом формате. Первая секция представляет набор моделей. Моделью называется совокупность пар префикса и постфикса. Ещё одна секция представляет набор корней с указателями соответствующую модель. Таким образом, достигается хороший процент сжатия словаря по сравнению с простым перечислением словоформ.

Лучше всего словарь можно представить в виде реляционной базы данных.

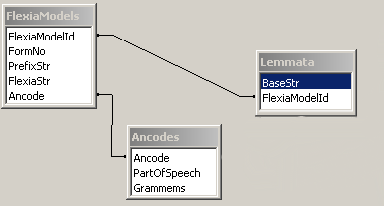
Словарь состоит из трёх частей: набор основ слов (Lemmata), набор возможных постфиксов (FlexiaModels) и набора дескрипторов (Ancodes). Взаимодействие этих частей показано на рисунке 3.1.

Рисунок 3.1. Схема морфологического словаря

2.5 Алгоритм анализа слова на возможные ошибки

Было рассмотрено несколько алгоритмов:

1) Расстояние Левенштейна.

2) Метод полных обратных преобразований.

3) Поиск максимальной подпоследовательности.

Расстояние Левенштейна и метод поиска максимальной подпоследовательности дают очень хорошие результаты при коррекции, однако имеют сложность зависимости от словаря больше линейной. Поэтому в работе был использован метод полных обратных преобразований. Для описания алгоритма необходимо дать несколько определений.

Определение: Отображение ошибки категории z = 1, 2 данной словоформы – множество словоформ, порождаемых этой словоформой в результате всех возможных ошибок категории z.

Выделяют два типа случайных ошибок:

1. удвоение символа (клаввиатура);

2. перестановка двух соседних символов (аглоритм).

Определение: Полное отображение одиночной ошибки данной словоформы – множество словоформ, порождаемых этой словоформой в результате всех возможных ошибок четырех категорий.

Таким образом, если через Г1 (словоформа) обозначить множество словоформ, порождаемых данной словоформой в результате ошибки категории 1 (отображение ошибки категории 1), через Г2 – отображение ошибки категории 2, через Г3 – отображение ошибки категории 3 и через Г4 – отображение ошибки категории 4, то полное отображение одиночной ошибки Г (словоформа) есть объединение всех четырех множеств.

Определение: Полное обратное отображение одиночной ошибки данной словоформы – множество словоформ, порождающих данную словоформу в результате одиночной ошибки из двух категорий.

Описание метода полных обратных преобразований:

1. Вносим в буквенную цепочку полное обратное преобразование.

2. Каждый из получившихся токенов проверяем на наличие в словаре.

3. Если токен имеется в словаре, то он добавляется в список корректных кандидатов.