Дипломная работа: Разработка системы Автоматизированное решение задач механики
Сопротивление материалов и теория упругости взаимопроникающи. Многое из того, что создано теорией упругости, воспринимается курсом сопротивления материалов и органически вписывается в его содержание.
Вместе с тем сопротивление материалов вследствие своей прикладной направленности решает задачи более широкие, чем математическая теория упругости. Но главное в том, что сопротивление материалов подводит инженера к неизбежным и вечным вопросам, на которые порой трудно ответить: выдержит ли конструкция или не выдержит, и какова степень ее надежности…
В теории упругости такие вопросы не рассматриваются.
Рассмотрим стандартные подходы к решению, с помощью методов сопротивления материалов, следующих задач [3]:
центральное растяжение-сжатие прямых стержней;
кручение валов;
плоский изгиб балок;
плоский изгиб рам.
Рассмотрим пошаговую процедуру решения задач центрального растяжения-сжатия прямых стержней:
жесткая заделка заменяется реактивной силой, значение которой находят из первого уравнения статики: ΣFx =0;
применяется метод РОЗУ (разделяем, отбрасываем, заменяем, уравниваем);
конструкция делится на сечения;
при рассмотрении одного сечения отбрасываются остальные, а их действие на рассматриваемое заменяется реактивной силой, определяемой из 1-го уравнения статики. Исходя из определенных реактивных сил определяется растяжение/сжатие на данном участке. Суммирование по участкам дает общее растяжение/сжатие.
Рисунки 1.1, 1.2, 1.3 поясняют смысл метода РОЗУ.
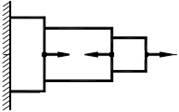
Рисунок 1.1 - Общий вид модели
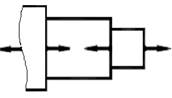
Рисунок 1.2 - Замена жесткой заделки реактивной силой
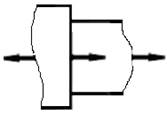
Рисунок 1.3 - Отбрасывание сечения и замена его действия реактивной силой
Рассмотрим пошаговую процедуру решения задач кручения валов:
из уравнения жесткости находится неизвестный крутящий момент;
вал разделяется на участки, применяется метод РОЗУ и определяются углы закручивания на каждом участке.
Рассмотрим пошаговую процедуру решения задач плоского изгиба балок:
из 2-го уравнения статики находится уравнение взаимосвязи между реакциями, подставляя которое в уравнение моментов, составленное относительно одной из опор определяются значения реакций.
применяя метод РОЗУ, определяют значения поперечной силы и изгибающего момента на каждом из участков, строят их эпюры, исходя из которых, определяют опасные сечения.
Рассмотрим пошаговую процедуру решения задач плоского изгиба рам:
из 2-го уравнения статики находится уравнение взаимосвязи между реакциями, подставляя которое в уравнение моментов, составленное относительно одной из опор определяются значения реакций.
применяя метод РОЗУ, определяют значения продольной, поперечной силы и изгибающего момента на каждом из участков, строят их эпюры, исходя из которых, определяют опасные сечения.