Дипломная работа: Разработка системы учета и прогнозирования ежедневных поступлений страховых взносов на обязательное пенсионное страхование
,
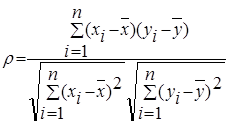где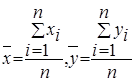 
,
и 
¾ среднее арифметическое значение соответственно по x и y.
Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе 
к 1, тем теснее линейная связь между x и y.
В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.
Корреляционное отношение вычисляется по формуле:
Формула 6
,
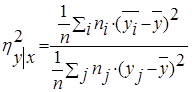где 
, а числитель характеризует рассеяние условных средних 
около безусловного среднего 
.
Всегда 
. Равенство 
соответствует некоррелированным случайным величинам; 
тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина 
используется в качестве индикатора отклонения регрессии от линейной.
Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные вводится еще одна характеристика ¾ коэффициент детерминированности.
Для его описания рассмотрим следующие величины.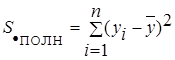 
- полная сумма квадратов, где среднее значение 
.
Можно доказать следующее равенство
Формула 7
.
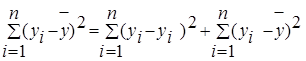Первое слагаемое равно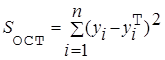 
и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.
Второе слагаемое равно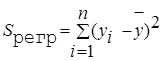 
и называется регрессионной суммой квадратов и оно характеризует разброс данных.
Очевидно, что справедливо следующее равенство
.
Коэффициент детерминированности определяется по формуле:
Формула 8
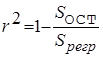
Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности 
, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y . В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае когда выполняется равенство 
то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.
1.3.2 Анализ методики расчета параметров уравнения аппроксимации
Имеются данные о поступлении платежей на страховую и накопительную части трудовой пенсии в апреле 2008-2009 гг. Требуется подобрать наилучшее аппроксимирующее уравнение для прогнозирования подневных доходов на 2010 год.
Таблица 1.2 - Данные о ежедневных платежах за март 2008-2009 гг.
|
2009 год |
2008 год | ||||||
|
0201 |
К-во Просмотров: 299
Бесплатно скачать Дипломная работа: Разработка системы учета и прогнозирования ежедневных поступлений страховых взносов на обязательное пенсионное страхование
| ||||||