Транспорт / Дипломная работа: Розробка, дослідження системи керування на основі нейронної мережі

Дипломная работа: Розробка, дослідження системи керування на основі нейронної мережі

Існують й інші критерії. Так, у роботах [9 –10] розглянуто новий підхід до аналітичного конструювання лінійно-квадратичних систем керування або, як їх називають у зарубіжних джерелах, задач лінійно-квадратичної оптимізації. Ці системи керування, на відміну від традиційних критеріїв, синтезуються без урахування конкретного критерію. Однак доводиться, що отримані системи керування завжди забезпечують мінімізацію деякого критерію. Це ж відмічається і в роботі [10], що функціонал, який оптимізує, не обов’язково постулювати. Він може являтися деякою супроводжуючою інтегральною оцінкою якості перехідних процесів. Така властивість притаманна критерію якості в методі аналітичного конструювання за критерієм узагальненої роботи. Складові частини функціоналу є інтегральною оцінкою якості перехідних процесів, точності стабілізації бажаного незбуреного стану, «витрат» керування або енергетичних витрат.

Сьогодні для синтезу оптимальних систем керування нелінійними об’єктами відомий цілий ряд методів.

Одним з найбільш відомих та вживаних методів оптимального керування є принцип максимуму Понтрягіна [11]. Переваги принципу максимуму проявляються там, де можна одразу, по одному виду гамільтоніана H знайти функції, на яких він сягає максимуму. Це можна зробити тоді, коли і функціонали і керування зв’язку або лінійні як відносно керувань, так і відносно фазових координат, або лінійні хоча б відносно керувань. У загальному випадку, який-небудь функціонал, екстремуми якого ми шукаємо, або рівняння зв’язку нелінійні по керуванню U(t), безпосередньо з виду гамільтоніана вже не можна судити про функції U(t), на яких він сягає максимуму.

Основна трудність рішення задач оптимального керування за допомогою принципу максимуму Понтрягіна, як і в методі динамічного програмування, запропонованого Р.Беллманом, полягає в рішенні двохкрапкової крайової задачі [12].

Відоме також значне число поодиноких методів класичного варіаційного числення, що придатні для вузьких класів задач оптимального керування [12]. Ці методи зручні для рішення задач оптимального керування, де управління шукаються у вигляді гладких або кусочно-гладких кривих, що не містять точок з нескінченними значеннями перших похідних, а також методи аналітичного конструювання регуляторів за критерієм узагальненої роботи (АКУР), де основна трудність пов’язана з визначенням коефіцієнтів функціонала, який оптимізується. Однак в теперішній час цю проблему можна вирішити за допомогою сучасних методів синтезу систем на основі нейромережевих технологій та методів нечіткої логіки.

Останні десять років інтенсивно розвиваються методи синтезу систем керування на основі векторного управління, методів нечіткої логіки, нейронних мереж та нейронечітких мереж [13– 14].

У цих роботах [16-18] з одного боку нечіткі системи керування використовуються для об’єктів управління, модель яких невідома, а з другого – як альтернатива класичним системам керування. Показано, що важливою перевагою нейромережевих систем керування є можливість їхнього навчання на прикладах. Тут же приведено ряд можливих архітектур для побудови нейромережевих систем управління.

Побудова систем векторного керування асинхронними електроприводами розглянуто в ряді публікацій [19-21]. У [19,20] розглянуті загальні принципи векторного управління електроприводами, зокрема, побудова систем векторного керування з використанням стандартних П-, ПІ-, ПІД-регуляторів. Найбільш повно методи застосування сучасних засобів штучного інтелекту (нечіткої логіки, нейронних мереж) в керування електроприводами описані в роботах [21,22]. Однак тут недостатньо уваги приділено питанням побудови моделей систем керування з використанням нечіткої логіки для конкретного типу електроприводу та проведення порівняльного аналізу з відомими системами, що містять стандартні регулятори.

Типова структура модуля нечіткої системи управління приведена на рисунку 1.2.

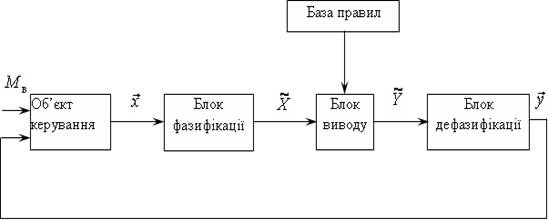
Рис. 1.2. Структура моделі нечіткої системи керування.

Інформація з об’єкта управління у вигляді чітких значень фазових координат об’єкта управління поступає на блок фазифікації, який на основі чітких значень вхідних змінних формує нечіткі значення відповідних лінгвістичних змінних. Блок виводу на основі правил вигляду:

де - відповідно нечіткі значення вхідних змінних та управлінь, визначає нечіткі управління , які за допомогою блоку дефазифікації перетворюються на вектор чітких управлінь , який впливає на виконавчі пристрої об’єкта керування за метою компенсації зовнішніх впливів M_E .

Зазвичай нечіткі системи керування застосовуються у випадках, коли модель об’єкта невідома.

Системи керування на основі штучних нейронних мереж багатьма авторами розглядаються як альтернатива класичним системам керування. У наш час відомий цілий ряд можливих архітектур побудови нейромережевих систем керування [23-24]. Великий інтерес до нейромережевих систем керування пов’язаний з тим, що вони мають ряд корисних властивостей, яких складно досягти за допомогою інших методів. Зокрема, мова йде про робастість систем керування, про визначення управлінь в умовах, коли неточно відома модель об’єкта про більш гнучке реагування на мінливі зовнішні умови та можливість обробки даних різної природи. Можна також відмітити, що для нейромережевих моделей не існує обмежень, пов’язаних з лінійністю системи або видом застосовуваного функціонала. Важливою перевагою нейромережевих систем керування є також можливість їхнього навчання на прикладах.

До істотного недоліку нейромережевих систем управління слід віднести недоступність знань, накопичених в системі та розподілених між усіма нейронами, зовнішньому спостерігачеві. Частково цей недолік подоланий у нейронечітких системах управління, які, з одного боку, використовують нечіткі правила виробки рішень, а з іншого – володіють здатністю до навчання.

В результаті можна відмітити, що виходячи з особливостей розглянутого об’єкта та характеристик методів оптимізації, найбільш доцільно використовувати для розробки системи управління методи нечіткої логіки та методи на основі нейромережевих технологій.

2. РОЗРОБКА МОДЕЛІ СИСТЕМИ КЕРУВАННЯ ЕЛЕКТРОПЕРЕДАЧІ ДИЗЕЛЬ-ПОТЯГУ

2.1. Моделювання тягових двигунів дизель-потягу

Даний розділ присвячено питанням розробки математичної моделі системи керування енергетичної системи дизель-потягу з тяговими асинхронними двигунами та їхній технічній реалізації з використанням комп’ютерних та інформаційних технологій. Серед розглянутих моделей приведені результати розробки моделей тягових двигунів з урахуванням їхнього використання для рішення задач синтезу регуляторів та дослідження об’єкту в цілому, моделей пристроїв формування керуючих впливів для випадків представлення ТАД у нерухомій двохфазній та трифазній системі координат, моделей регуляторів САК, системи керування та їхніх функціональних схем із врахуванням технічної реалізації, результати дослідження моделей та визначення адекватності.

У якості тягового асинхронного двигуна в системі, що моделюється, приймається ідеалізована машина з симетричною системою обмоток статора і ротора, гладким повітряним зазором, синусоїдальним розподілом магнітного потоку уздовж окружності статора і ротора, при роздільному обліку насичення по головному шляху магнітного потоку та по шляхам розсіювання, без урахування ефекту витіснення струму в обмотках ротора та втрат сталі [25].

Об’єкт дослідження в загальному вигляді може бути представлений системою диференційних рівнянь, що описують електромагнітні процеси ТАД як у прямокутній системі координат α, β, так і в природній (в осях a,b,0) [26].

Математична модель електроприводу у нерухомій прямокутній системі координат у осях α і β описується системою диференціальних рівнянь (2.1), що приведені нижче [26, 27].

(2.1)