Дипломная работа: Розробка Штормового родовища

(2.20)

Неусталений режим фільтрації

Обробка даних дослідження свердловин при неусталеному режимі фільтрації базується на теорії пружності пластової системи. Закономірності кривих відновлення тиску після зупинки свердловин, виведені з основних теоретичних положень пружного режиму знайшли універсальне застосування в промислових дослідженнях свердловин.

Усі методи досліджень виходять з наступних: приймається, що перед зупинкою дебіт свердловини усталений, тиск довкола неї розподілився за стаціонарним законом, пласт характеризується постійною потужністю і однорідною проникністю; приплив однофазний.

Найбільш простий аналітичний вираз кривої відновлення вибійного тиску отримано для свердловини в необмеженому однорідному пласті зупиненої після роботи на стаціонарному режимі радіальної фільтрації при повній відсутності припливу після зупинки (формула запропонована М.Маскетом для точкового джерела в необмеженому пласті):

(2.21)

де — біжучий дебіт свердловини перед зупинкою; (-х) – інтегральна експоненційна функція; Т - час припливу рідини (або газу) до свердловини; t – час відновлення пластового тиску; χ – п'єзопровідність.

Приплив рідини з пласта після закриття свердловини поступово припиняється і пісдя деякого часу крива відновлення вибійного тиску наближається до кривої підвищення тиску у свердловині після її раптової зупинки.

Обробка при даному припущенні проводиться за методом Хорнера, методом дотичної.

Практика визначення параметрів пласта і свердловини показала, що не завжди за 2-3 години не вдається отримати криву відновлення тиску, тобто не встигає сформуватись прямолінійна ділянка лінії . Крім того форма кривих відновлення тиску при наявності притоку в свердловину така, що практично завжди можна виділити прямолінійний відрізок і прийняти помилково його за асимптотичну пряму, яка відповідає фільтраційним властивостям пласта. Щоб цого уникнути, запропоновані методи для обробки кривих, які використовують початкову ділянку (метод Ю.П. Борисова, метод Чарного-Умрихіна, метод Е.Б. Чекалюка, метод детермінованих моментів).

В основу методу Хорнера взято рівняння (2.21), яке перетворене таким чином

(2.22)

В системі координат , рівняння (2.22)має вид прямої лінії за нахилом якої

(2.23)

визначають гідропровідність

(2.24)

При нескінчено тривалій зупинці у свердловині відновиться тиск до пластового, бо при t величина . В цій точці знаходиться максимальне значення депресії, а повністю відновлений пластовий тиск буде рівний

Р_пл =Р_в +∆Р_max

де Р_в – усталений тиск на вибої перед зупинкою свердловини.

Розглянемо метод детермінованих моментів (МДМ). Детерміновані моменти являють собою інтегральні характеристики КВТ:

(2.25)

де n = 0; 1; 2.

Нульовий Мо, перший М₁ , другий М₂ моменти визначають як інтеграл за часом t від поточної депресії тиску з вагою t °, t ¹ , і t ² відповідно.

Інтеграл (2.25) можна представити у вигляді суми двох інтегралів: від 0 до t_мах і від t_мах до де t_мах – повний час заміру КВТ

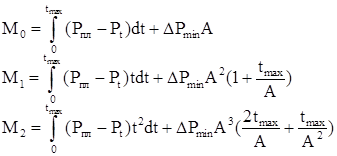(2.26)

де , А – коефіцієнт ідентифікованого рівняння першого порядку

(2.27)

При цьому похідна () обчислюється методом кінцевих різниць, після чого для тих самих діюх часових точок виписується система лінійних алгебраїчних рівнянь, яка розв'язується відносної А і Р_пл . Таким чином, у значній мірі враховується частка детермінованих моментів, яка припадає на недовідновлену частину КВТ і зменшується викривляючий вплив від обмежності часу проведення гідродинимічних досліджень в реальних промислових умовах.

Що стосується перших інтегралів рівнянь М₀ , М₁ , то вони обчислюються методом трапецій: