Дипломная работа: Сусловарочный аппарат

где

n _меш. -частота вращения мешалки, с^-1 , n _меш. = 0,67 с^-1 .

- вязкость сусла, определяем как вязкость суспензии, состоящей из взвешенных твердых частиц и воды:

, (2.17)

где μ_в – коэффициент динамической вязкости воды, Па·с;

- объемная доля дисперсной фазы, м³ /м³ . ε<0,1 , примем ε=0,06.

При средней температуре кипения сусла t=105 (по условию)

μ_в =0,269 10^-3 Па

Тогда

Согласно формуле (2.16) критерий Рейнольдса мешалки равен:

Критерий Прандтля находят по формуле:

, (2.18)

где λ_сусла – коэффициент теплопроводности сусла

λ_сусла = 0,635 Вт/(м·К)

С_сусла – удельная теплоемкость сусла, кДж/(кг·К)

Удельная теплоёмкость сусла равна:

, (2.19)

где С₀ – удельная теплоемкость сухих веществ, С₀ = 1,42 кДж/(кг·К);

С_в – удельная теплоёмкость воды, С_в = 4,19 кДж/(кг·К);

W _н – содержание влаги в начальном сусле, %.

W_н = 100-В_н =100-9,5=90,5%

Тогда

. 1

Коэффициент динамической вязкости при температуре стенки аппарата

t _ст = 128,9 ^о С:

1

А значит критерий Нуссельта, исходя из формулы (2.12) равен:

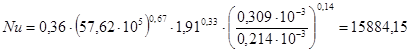
1

А по формуле (2.11):

Коэффициент теплоотдачи от греющего пара к стенке с учетом потерь теплоты за счет образующегося на внутренней поверхности аппарата осадка

по формуле (2.6) равен:

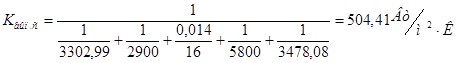
Исходя из проделанных выше расчетов определяем необходимую площадь поверхности нагревания сусловарочного аппарата по формуле (2.3) равна:

Площадь поверхности теплопередачи на 1м³ полезной вместимости аппарата со стальным днищем:

(2.20)

Так как полученная удельная площадь поверхности теплопередачи больше, чем F_кот1 =1,2 , считаем, что аппарат работает в нормальных условиях.

3. Определение расхода пара

Расход пара в аппарате определяем из уравнения теплового баланса:

, (3.1)