Дипломная работа: Управление кредитными рисками в банковской системе Российской Федерации и способы их снижения на

В связи с этим при анализе кредитного риска необходимо оценивать его с двух позиций как EL и UL. Ожидаемые потери вычисляются по вероятностям неплатежеспособности (дефолтов) компанийзаемщиков, а также по величинам обеспечения по кредитам. Величина ожидаемых потерь напрямую влияет на прибыль от кредитного продукта, поскольку необходимо отчислять страховую сумму в резервный высоколиквидный фонд с каждого кредита, эта сумма должна быть не менее величины EL. Величина неожидаемых потерь по портфелю также косвенно влияет на прибыль от кредитной деятельности, поскольку определяет собственный уровень надежности кредитного портфеля и банка в целом. Собственный уровень надежности определяется соответствием капитала возможным неожидаемым потерям, которые могут произойти с вероятностью дополняющей до полной вероятность (уровень) надежности. Для оценки величины UL требуется построение кривой потерь по портфелю, что является нетривиальной задачей. Базельский комитет в своих требованиях банкам считает нужным внедрение методик внутреннего рейтингования заемщиков банка и кредитных продуктов, что предполагает умение оценивать величины, отвечающие за риск потерь. Это, прежде всего, PD cреднегодовая вероятность дефолта заемщика с известной датой расчета, LGD (Loss given default) средне ожидаемая доля потерь средств в случае дефолта, M (Maturity) длина кредита, EAD (exposure at default) величина средств под риском. На риск портфеля также влияет и групповая принадлежность заемщиков, через возможную корреляцию между дефолтами. Согласно современным требованиям Базельского комитета уровень надежности должен быть не менее 99%.

Одной из основных и нетривиальных задач в оценке риска это задача вычисления вероятности дефолта заемщика. Мы имеем два подхода к вычислению PD. Первый основан на качественной и количественной оценке рейтинга заемщика по его внутренним финансовым показателям и особым бизнесфакторам. Второй основан на капитализации заемщика на фондовом рынке и уровне его долгов перед кредиторами. К сожалению, второй подход, хоть и является наиболее объективным, применим лишь к небольшому числу российских открытых компаний.

При количественном анализе риска под риском принято понимать вероятность, угрозу потери предприятием части своих ресурсов, недополучения доходов или появление дополнительных расходов в результате осуществления определенной производственной и финансовой деятельности [33, с.16] .

Величину риска в абсолютном выражении будем обозначать буквой W.

W=Р_{H *} x(1.1)

гдеР_H – вероятность наступления неблагоприятных последствий,

x – величина этих последствий.

Наиболее вероятное значение абсолютного риска представляется как:

W=M(X)=M_X =m_X (1.2)

где Мх – математическое ожидание неблагоприятных последствий (прибыли).

Статистический разброс вероятных значений риска относительно матожидания оценивается величиной DW

DW=D(X)=s² _X (1.3)

где D(x) – рассеивание значений случайной величины вокруг среднего значения (дисперсия);

s(х) – среднеквадратическое отклонение от матожидания.

Если считать, что X₁ и X₂ – величина прибыли, то при m₁ >m₂ и s₁ <s₂ более привлекательная ситуация, характеризующаяся случайной величиной X₁ .

Риск в относительном выражении определяется как соотношение максимально возможного объема убытка и объема собственных финансовых ресурсов (коэффициент риска):

, (1.4)

где Х – размер максимально возможных убытков,

C – объем собственный финансовых ресурсов с учетом точно известных поступлений средств.

Алгоритм определения риска получения результата Х при наличии расчетной или опытной выборки результатов определяется в следующей последовательности [32, с.34]:

а) Выборка результативных признаков представлена последовательностью n значений Xi ( I=1,…,n) .

б) Среднее арифметическое значение выборки определяется по формуле :

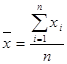(1.5)

в) Стандартное среднеквадратическое отклонение в выборке от среднего определяется по формуле :

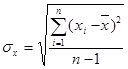(1.6)

г) Дисперсия выборки (при n<50) определяется по формуле :

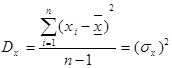(1.7)

д) Коэффициент вариации результатов выборки определяется как :

(1.8 )

е)Граничное отклонение средней величины от матожидания результата Х (абсолютный риск отклонения результата) определяется по формуле :

, (1.9)

где дисперсия выборки,

n1 – число степеней свободы,

t – коэффициент доверия выборки(квантиль), который зависит от

вероятности доверия и объема выборки.

Величины квантилей найдем по таблице удвоенной нормированной функции Лапласа) [33, с.247] :

При вероятности P=0,683 > t=1,00

При вероятности P=0,954 > t=2,00