Дипломная работа: Устройства генерирования и канализации субмиллиметровых волн

Режим ОНПЗ не связан с эффектом времени пролета, и частота генератора зависит в первую очередь от частоты настройки внешнего резонатора. Имеется возможность увеличить размеры прибора. При этом почти весь объем материала диода будет обладать отрицательной проводимостью. Вследствие этого мощность генераторов на диодах в режиме ОНПЗ увеличится на 4 - 6 порядков. Способ ограничения накопления пространственного заряда (режим ОНПЗ) основан на следующих явлениях.

Нарастание и спад (рассасывание) пространственного заряда происходят за конечное время, которое обратно пропорционально степени легирования материала полупроводника или концентрации носителей. Время нарастания пространственного заряда при величине поля, превышающей критический уровень возникновения отрицательной проводимости 3000 В/см, значительно больше, чем время спада (рассасывания), которое происходит, когда напряженность поля становится ниже критической. Таким образом, изменяя напряженность поля в диоде до уровня ниже критического на время, составляющее малую часть периода колебаний, можно осуществить рассасывание пространственного заряда, накопленного во время работы при напряженности, обеспечивающей появление отрицательного сопротивления.

Арсенидогаллиевый диод работает в режиме ОНПЗ, если выполняется условие

2*1014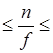2*1015 шс/см3 (1.1)

Следовательно, необходимо обеспечить весьма узкий интервал допустимых уровней концентрации примесей в материале диода.

Вторым условием установления режима ОНПЗ является высокий импеданс внешних по отношению к диоду резонансных цепей, обеспечивающих получение больших амплитуд колебаний на диоде. При этом необходимо, чтобы напряженность поля, приложенного к диоду, в 3 - 4 раза превышала значение напряженности поля, которому соответствует эффект Ганна. Достаточно высокие значения добротности могут быть получены установлением слабой связи резонатора с нагрузкой в момент возникновения колебаний; после этого нагрузку резонатора, выходную мощность и к. п. д. можно заметно увеличить. Отрезок линии передачи между резонатором и нагрузкой может обеспечить задержку момента нагружения резонатора.

Поскольку рабочая частота генератора в режиме ОНПЗ не зависит от толщины образца, можно увеличить длину и объем образца в несколько раз. При этом возрастает и приложенное напряжение. Так как мощность пропорциональна квадрату приложенного напряжения, то появляется возможность значительного повышения выходной мощности. Диод, работающий в режиме ОНПЗ, может быть сконструирован для работы при любом напряжении от 25 до 500 В.

Увеличению выходной мощности диодов с ОНПЗ препятствуют в основном трудности обеспечения хорошего теплоотвода и поддержания постоянной напряженности электрического поля по всей длине диода.

Кроме задач, связанных с разработкой самих диодов, стоят также задачи создания специальных конструкций генераторов, в особенности для субмиллиметровых волн, где найдут применение открытые резонаторы.

Примером тому может послужить генератор субмиллиметрового диапазона, в котором используются объемные эффекты в арсениде галлия. Основой генератора служит пластина арсенида галлия длиной 3 мм, шириной 1 мм и толщиной 0,5 мм с концентрацией носителей 1,2*1016 см-3. На концах пластины создаются оловянные омические контакты. На одной стороне пластины в середине ее вырезана канавка шириной 1 мм и глубиной 0,15 мм. На дне канавки нанесена пленка титаната бария, на которую напылен слой проводника. С другой стороны пластины нанесены пленки из титаната бария, на которых напылен слой проводящего материала. Емкостный электрод в канавке соединен с одним из омических контактов.

К крайним выходным электродам на другой стороне пластины подсоединен отрезок замкнутого накоротко коаксиального кабеля. При подаче на контакты импульсов длительностью 60 нсек с амплитудой 80—100 В возникали колебания, частота которых зависела от длины отрезка кабеля и изменялась в больших пределах. В частности, наблюдались колебания с частотой 380 Ггц. По мнению разработчиков, этот эффект не связан с режимом ОНПЗ. Предполагается, что колебания вызывает слой нейтрализуемого объемного заряда. В момент приложения напряжения к омическим контактам начинает образовываться и распространяться объемный заряд. Однако развитию этого процесса препятствует сильное поле, создаваемое управляющим электродом, что обеспечивает отрицательное сопротивление всего объема материала.

2. Резонансные системы субмиллиметрового диапазона

Резонаторы являются важнейшими элементами целого ряда генераторных и измерительных устройств миллиметрового и субмиллиметрового диапазонов. В длинноволновой части миллиметрового диапазона в качестве резонансных систем еще используются обычные объемные резонаторы. Однако по мере укорочения рабочей длины волны размеры объемных резонаторов, в которых может существовать один вид колебаний, существенно уменьшаются. Это вызывает снижение добротности вследствие возрастания отношения площади поверхности стенок резонатора к его объему. Кроме того, малые линейные размеры налагают очень жесткие требования на точность изготовления резонатора, которая практически не может быть достигнута.

Особенности резонансных систем субмиллиметрового диапазона

Повышение добротности резонатора путем увеличения объема приводит к сгущению спектра резонансных частот, резонансные кривые отдельных видов колебаний перекрываются и резонатор теряет селективные свойства.

В устройствах миллиметрового и субмиллиметрового диапазонов и в оптических квантовых генераторах (ОКГ) был применен оптический резонатор, являющийся аналогом известного в оптике интерферометра Фабри-Перо (ИФП). Это наряду с дальнейшим развитием теории таких резонаторов позволило преодолеть затруднения, возникшие при разработке приборов субмиллиметрового диапазона.

Первоначально в миллиметровом диапазоне был создан открытый резонатор с плоскими полупрозрачными зеркалами для работы с отраженным сигналом, несколько позднее Колшоу разработал открытый резонатор проходного типа, обладающий значительно лучшими характеристиками. Последний прибор представлял собой систему из двух многослойных зеркал, расположенных параллельно друг другу, расстояние между которыми изменялось в широких пределах. Было показано, что с помощью подобного устройства можно определять малые потери в диэлектриках и производить точные измерения длины волны. Добротность оптического резонатора превышала 50 000, что близко к значению добротности лучших образцов объемных резонаторов. Улучшение качества зеркал позволило применить проходной оптический резонатор для таких точных измерений, как, например, измерение скорости распространения электромагнитных волн в вакууме.

Успешное использование А.М. Прохоровым, А. Шавловым и Ч. Таунсом открытых резонаторов для удлинения времени взаимодействия электромагнитной волны с рабочим веществом в квантовом генераторе заинтересовала многих исследователей, которые занялись разработкой теории ИФП с учетом явлений дифракции, существенно влияющей на работу прибора даже в оптической области спектра. В начале 60-х годов появились работы Фокса и Ли, в которых задача определения распределения полей, спектра резонансных частот и радиационных потерь, обусловливающих совместно с джоулевыми потерями ненагруженную добротность резонатора, сводилась к решению однородного интегрального уравнения Фредгольма второго рода. Резонаторы типа ИФП стали называть открытыми вследствие того, что поверхность их зеркал значительно меньше поверхности, ограничивающей резонансный объем между зеркалами. Благодаря сильной связи большинства собственных видов колебаний с открытым пространством происходит разрежение спектра резонансных частот. Резкую границу между оптическим резонатором и открытым резонатором провести невозможно. Систему называют открытым резонатором, если при ее возбуждении элементарным диполем или малым отверстием в центре одного из зеркал наблюдаются резонансы. Если же резонансы наблюдаются только при возбуждении плоской волной и резонансные кривые отдельных видов колебаний перекрываются, то система работает как интерферометр.

В простейшем случае открытый резонатор состоит из двух плоских бесконечно тонких дисков, расположенных параллельно друг к другу так, что их оси симметрии совпадают.

Экспериментально установлено, что такие резонаторы имеют дискретный спектр резонансных частот и соответствующие им собственные колебания с малыми потерями на излучение в свободное пространство.

Следовательно, если задать начальное распределение поля на одном из зеркал и представить его в виде суммы собственных колебаний такой системы, и считать, что эти колебания имеют различную связь со свободным пространством, то через некоторый промежуток времени, затухая по экспоненциальному закону, колебания будут иметь тем меньшую амплитуду, чем больше аргумент экспоненциальной функции. В конце концов в резонаторе будет существовать с заметной амплитудой только один вид колебаний с распределением поля, которое обеспечивает минимальные радиационные потери. Это в некотором приближении соответствует задаче Коши, но в данном случае различная связь со свободным пространством полей различных видов колебаний дает возможность найти характеристики нормального вида колебания, при котором потери минимальны. Очевидно, эту задачу разрешить тем легче, чем ближе исходное распределение поля к искомому.

Если отвлечься от явлений дифракции на ребрах зеркал, что справедливо для резонаторов с размерами зеркал, значительно превышающими длину волны, то можно смоделировать описанный выше процесс фильтрации, заменив отражения волны от зеркал последовательным прохождением ее сквозь абсолютно черные диафрагмы с апертурой отверстия, равной апертуре зеркала. Процесс распространения волны от диафрагмы к диафрагме можно описать с помощью линейного интегрального оператора, который позволяет найти поле в любой точке по заданному распределению на какой-либо поверхности. Очевидно, что если в такой системе останется волна, которая соответствует одному из собственных видов колебаний открытого резонатора, то при последовательном прохождении диафрагм нормированное поперечное распределение поля не будет изменяться. Связь с открытым пространством вызовет лишь уменьшение общей энергии, переносимой волной. Эти соображения позволяют свести задачу о нахождении собственных видов колебаний открытого резонатора к однородному интегральному уравнению Фредгольма второго рода типа

, (2.1)

где v - поперечное распределение скалярного поля вблизи зеркала;

- константа, определяющая резонансные частоты и потери резонатора; интегрирование проводится по поверхности одного из зеркал.

В квазиоптическом приближении, когда

(2.2)

ядро интегрального уравнения упрощается, становится симметричным, но не эрмитовым:

(2.3)