Дипломная работа: Вивчення дифракції світла

Розглянемо теорію дифракції від однієї щілини. Теорія дифракції на одній щілині (отворі) має велике практичне значення при проектуванні мікроскопів і телескопів, вона потрібна для пояснення роздільної здатності дифракційних граток, а також для розуміння дифракційної природи оптичного зображення тощо. Якщо “вилучити” непрозорий проміжок між нескінченно тонкими щілинами, можна отримати щілину певної ширини a. Нехай ми маємо своєрідну щілину, що складається з n = 12 джерел, які випромінюють світлові хвилі. Відстань між крайніми джерелами дорівнює a, а між сусідніми — a₁ , причому l > a (мал.5). Дослідимо зміну картини, що спостерігається на екрані від щілини певної ширини, залежно від просторового кута при незмінному положенні екрана і щілини. Ті промені, для яких q =0, збираються лінзою або інтерферують у нескінченності в точці Р₀ , оскільки сумарна напруженість Е₁ =n E₀ . Виберемо такий напрям поширення променів, при якому різниця ходу між крайнім і середнім променями дорівнює . Тоді між крайніми променями ця різниця дорівнює l. З мал.5 видно, що від першого осцилятора, який знаходиться у нижній половині щілини, результуюча напруженість дорівнює нулю. Крім того, такі пари осциляторів, як 2 і 8, 3 і 9, 4 і 10, 5 і 11, 6 і 12 в точці Р також створюють результуючу напруженість, що дорівнює нулю (коливання від цих пар осциляторів різняться на 180°). З мал. 5 видно, що a=a₁ n, бо n>>1. Умову першого мінімуму (“нуля” інтенсивності хвилі) можна записати так:

(4)

Тому в напрямі, для якого різниця ходу між крайнім і середнім променями дорівнює половині довжини хвилі, тобто , має місце перший мінімум. Умову першого мінімуму перепишемо так: a sinq₁ = l .

Отже, якщо різниця ходу між крайніми хвилями дорівнює довжині хвилі, має місце мінімум напруженості в точці Р. Для малих кутів (q≤30°)

(5)

Прийом попарного додавання миттєвих значень напруженості двох світлових хвиль є найпростішим способом встановлення кінцевого результату дифракції від багатьох пар “точкових джерел” щілини.

Слід підкреслити, що кожній точці (зоні) верхньої половини щілини відповідає деяке джерело (зона) з нижньої половини, і їх дії взаємно компенсуються. Отже, умовою першого мінімуму є наявність у щілині парного числа зон, які компенсують одна одну. Ці зони називають зонами Френеля. Зони Френеля – це уявні вузенькі смужки хвильового фронту щілини, різниця відстаней від відповідних (крайніх) точок яких до екрана дорівнює . Ширина зони x₁ визначається за умови тобто

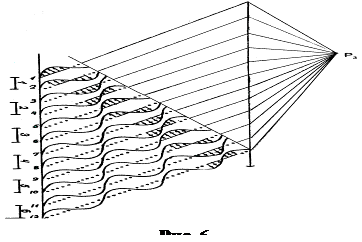
Виберемо тепер напрям, для якого різниця ходу між середнім і крайнім променями дорівнює l, а між крайніми – 2l. Отже, різниця ходу між сусідніми хвилями при цьому становить j =60° (Рис.6). У даному разі різниця фаз 180° буде спостерігатися для таких пар осциляторів: 1 і 4, 2 і 5, 3 і 6 (четвертий скомпенсований першим, п’ятий – другим, шостий - третім). Таким чином, маємо чотири зони. Перша, в яку входять джерела 1,2,3, нейтралізується другою (джерела 4,5,6), третя зона, що складається із джерел 7,8,9, компенсується четвертою (джерела 10,11,12).

Для кута q₂ щілину можна уявити як сукупність чотирьох зон Френеля : a =4x₂ . (Тому різниця ходу визначається кількістю зон Френеля: ∆l=4x₂ ). При цьому ширину знаходять із співвідношення: або

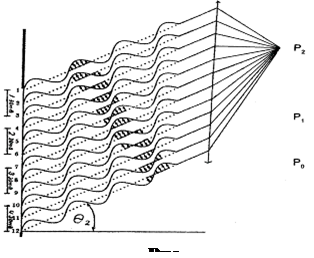
Для випадку 3l=asinq₃ відстані між сусідніми джерелами відповідають зсуву фаз на 90° (мал.7). Виділимо ті пари джерел, хвилі від яких відрізняються на 90°: третє джерело компенсується першим, четверте – другим, сьоме – п’ятим, восьме – шостим тощо.

Залишається шість зон, у які входять відповідно джерела 1 і 2, 3 і 4, 5 і 6, 7 і 8, 9 і 10, 11 і 12. Ширину зони у цьому разі знаходять із співвідношення:

Отже, при інтерференції світла від кожної пари із сусідніх зон амплітуда результуючих коливань дорівнює нулю, оскільки вони в цілому викликають коливання з однаковими амплітудами, але протилежними фазами. Тому умову мінімуму інтерференції можна визначити, по – перше, за парним числом півхвиль, що вкладаються в різницю ходу між крайніми променями, а саме:

де m= 1,2,3,…, а, по – друге, через парне число зон Френеля в щілині: або (6)

Встановимо геометричну умову для пучностей. У напрямі q=0 спостерігається найінтенсивніший центральний максимум нульового порядку: коливання, що викликаються всіма ділянками щілини, здійснюються в однаковій фазі. Далі будемо міркувати так. Якщо різниця ходу між крайніми променями дорівнює l, в щілині(отворі) вкладається дві зони, які компенсують одна одну, а якщо різниця ходу між крайніми променями дорівнює , то в щілині(отворі) вкладається одна зона, яка нічим не компенсується. Це означає, що у випадку однієї зони різниця ходу ∆l між середнім і крайнім променями дорівнює , тобто (7)

Щілина (отвір) відкриває одну зону, й інтенсивність світла в центрі дифракційної картини в 4 рази більша, ніж за відсутності щілини (отвору). Перший побічний максимум повинен бути в напрямі між першим і другим дифракційними мінімумами і визначатися з умови тобто

Тому різниця фази між сусідніми джерелами становить

Відмітимо пари джерел, різниця фаз між якими становить 180°. Це такі: 1 і 5, 2 і 6, 3 і 7, 4 і 8. Оскільки джерела 5, 6, 7,8 уже скомпенсовані, залишаються не скомпенсованими джерела 9, 10, 11, 12. Таким чином, зона (1, 2, 3, 4) компенсується зоною (5, 6, 7, 8), а зона (9, 10, 11, 12) дає побічний максимум, інтенсивність якого становить 1/3 від інтенсивності всієї щілини. І в цьому разі дифракційний максимум першого порядку відповідає дії однієї зони (промені 9, 10, 11, 12). Аналогічно можна показати, що умови дифракційного максимуму запишуться через непарне число півхвиль, що вкладається в різниці ходу між крайніми променями, або через непарне число зон Френеля, що вміщуються у щілині: (8)

(9)

Порівняємо ширину головного (нульового) максимуму на екрані із шириною наступних максимумів. Нехай - відстань від середини центрального (нульового) максимуму до першого мінімуму, а - відстань від тієї ж середини центрального максимуму до другого мінімуму (Рис.8). Тоді , ширина головного максимуму становить , а ширина першого максимуму .

Отже, ширина нульового максимуму інтенсивності при вдвічі більша від наступних, перших максимумів, розміщених симетрично, тобто . Із виразу для видно, що червоне світло дифрагує сильніше, ніж синє.

2.2. Умови чіткого спостереження дифракції від однієї щілини

Характерною ознакою дифракції від щілини є те, що ширина нульового максимуму D_o на екрані вдвічі більша від наступних, перших максимумів, розміщених симетрично:

, (10)

де - ширина щілини. Формула для обчислення інтенсивності світла на екрані від однієї щілини:

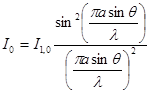(11)

Ми дотримуємось тієї позиції, що у широкому розумінні дифракція - сукупність явищ, зумовлених хвильовими властивостями світла, при яких порушуються закони геометричної оптики. Виділимо деякі з них.

Одним із явищ, які пояснюються на основі хвильової теорії, є прямолінійне поширення світла. Нехай від світної точки S світло поширюється у вигляді сферичної хвилі і доходить до точки А. За принципом Гюйгенса із точки А ми повинні бачити кожну точку сферичної хвилі. Однак цього не відбувається. Адже згідно із принципом Френеля коливання, які доходять до точки А від різних точок сферичної поверхні, взаємно знищуються, бо для кожної точки поверхні знайдеться інша точка, хід хвилі від якої до точки А відрізнятиметься на половину довжини хвилі, і вони гасяться. Отже, прямолінійне поширення світла належить до тих явищ, які можна пояснити, виходячи із принципу Гюйгенса-Френеля.