Дипломная работа: Влияние температуры и магнитного поля на электрическую проводимость и аккумуляцию энергии в конд
В более общем случае для двух носителей ![]() , где знаки «+» и «-» относятся к положительным и отрицательным носителям соответственно.
, где знаки «+» и «-» относятся к положительным и отрицательным носителям соответственно.
Т.к. ![]() , (m – подвижность), то
, (m – подвижность), то ![]() , считая, что
, считая, что ![]() , и что
, и что ![]() , то
, то ![]() , где s - коэффициент электропроводимости.
, где s - коэффициент электропроводимости.
Наряду с током, обусловленным дрейфом, возникает диффузионный ток с плотностью
![]() ,
,
где r з – объемная плотность заряда, равная gn , D – коэффициент диффузии, определяемый соотношением Нернста-Эйнштейна.
![]() ,
,
тогда полный ток составит (в случае носителей одного знака)
![]() ;
;
![]() .
.
При условии продолжительного действия поля E наступает динамическое равновесие, при котором ![]() :
:
![]() .
.
Отсюда нетрудно получить с учетом ![]() для одномерного случая
для одномерного случая ![]() , что
, что
![]() или
или ![]() .
.
После интегрирования можно получить
![]()
здесь ![]() – значение r при
– значение r при ![]() .
.
Разделение носителей заряда неоднородно ввиду различия их состава, массы, подвижности. Поэтому и m , и E являются функциями координат. Среднее значение плотности тока по толщине кондуктометрической ячейки КЯ вдоль оси ОХ, перпендикулярной площади электродов будет
 ,
,
причем, согласно уравнению Пуассона
![]()
для одномерного случая ![]() .
.
Если в КЯ находятся и свободные и связанные (фиксированные) заряды r св и r связ , то
 ,
,
отсюда ![]() .
.
Тогда, считая для простоты ![]() , можно записать:
, можно записать:
 .
.
Пусть граничными условиями будут:
1. при ![]()
![]() ;
;
2. при ![]()
![]() ,
,
тогда, так как

 ,
,
![]() – приращение потенциала, то
– приращение потенциала, то
![]() .
.
Это выражение можно преобразовать
![]() ,
,
![]() – суммарное поле внутри КЯ. Это легко связать с поверхностной плотностью s * зарядов обоих типов
– суммарное поле внутри КЯ. Это легко связать с поверхностной плотностью s * зарядов обоих типов ![]() .
.
В то же время ![]() учтя это, можно получить
учтя это, можно получить


Поведение ![]() можно оценить по ее производной. Пусть
можно оценить по ее производной. Пусть ![]() , тогда
, тогда ![]() и
и ![]()
![]() .
.
При этом МЖ должна быть нейтральной. Пусть полный заряд ![]()
Тогда ![]() ,
, ![]() по модулю.
по модулю.
Но тогда ![]() и
и ![]() .
.
 Т.к.
Т.к. ![]() и
и ![]() , где v – объем КЯ и
, где v – объем КЯ и ![]() , S – площадь, то
, S – площадь, то ![]() , т.к.
, т.к. 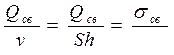 , а
, а ![]() , тогда
, тогда ![]() .
.
![]() .
.
Это линейная функция, где C ¢ имеет смысл удельной электропроводности s . Следовательно, если ток протекает, то он должен подчиняться закону Ома (см. рис.).
Перенос электрического заряда в КЯ при пропускании электрического тока