Дипломная работа: Выращивание плёнки GeSi и CaF2 на кремниевых подложках

Задача получения совершенных, полностью релаксированных пленок GeSi/Si распадается на две подзадачи: а) обеспечить приемлемый темп релаксации пленки введением ДН; б) свести до минимума количество прорастающих дислокаций. В определенной степени эти две подзадачи противоречивы, так как введение ДН происходит через прохождение ПД через объем пленки.

1.1.2 Критическая толщина введения дислокаций несоответствия

Еще в 1949 г. Франк и Ван дер Мерве [3] указали на возможность выращивания тонкого кристаллического слоя на подложке с иным параметром решетки без дефектов на границе раздела. В такой гетеропаре рассогласование параметров решеток пленки и подложки компенсируется изменением размеров ячейки слоя. В результате этого слой оказывается биаксиально напряженным, а его граница раздела когерентно сопряжена с подложкой. Энергия деформаций, накапливающаяся в пленке, пропорциональна её толщине. После того, как толщина слоя начинает превосходить некоторую величину, называемую критической толщиной, энергия становится настолько большой, что на границе раздела возникают дислокации несоответствия, частично или полностью снимающие напряжения в объеме пленки.

1 .1.3 Модель энергетического баланса

Мэтьюзом была предложена модель энергетического баланса (energybalancemodel) [4], которая основана на сравнении энергий напряжённой и пластически релаксированной плёнок. Энергия напряжений единицы площади псевдоморфной пленки толщиной h есть

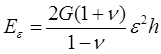(1)

где G и ν– соответственно модуль сдвига и коэффициент Пуассона в изотропном твёрдом теле, ε – двумерная (плоская) упругая деформация в пленке, возникающая из-за разницы параметров решетки пленки и подложки:

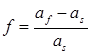(2)

Энергия единицы площади сетки дислокаций несоответствия, пластически релаксирующих пленку, равна

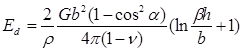(3)

Здесь множитель 2 отвечает двум системам дислокаций несоответствия в каждом направлении <110> вдоль границы раздела, ρ – количество дислокаций на единицу длины в плоскости границы раздела, b – величина вектора Бюргерса дислокации, а α – угол между вектором Бюргерса и линией дислокации. Число β называется параметром ядра дислокации и для системы GeSi по современным данным принимается равным 0,76 (для 60°-ных дислокаций) [7]. Количество дислокаций ρ, участвующих в пластической релаксации пленки, равно

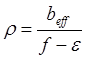(4)

где b_eff – эффективный вектор Бюргерса (т.е. компонента вектора Бюргерса, лежащая в плоскости границы раздела в направлении, перпендикулярном ДН – величина абсолютной пластической релаксации, являющаяся следствием появления одной ДН). Тогда

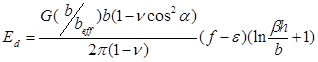(5)

Полная энергия пленки равна E_ε +E_d . Величина упругих деформаций пленки, ε^* , при которых эта сумма минимальна, может быть определена из выражения d(E_ε +E_d )/d_ε =0, и она равна

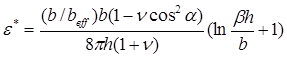(6)

Наибольшая возможная величина для ε^* равна f. Таким образом, толщина псевдоморфной пленки, при которой становится возможным появление первых ДН, - критическая толщина, равна

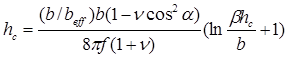(7)

Для сетки краевых дислокаций α = 90° и b/b_eff =1. Для 60°-ных дислокаций α = 60° и b/b_eff .= 2. С учетом того, что для системы GeSi ν = 0,28, f = 0,041.x (x – доля Ge в твердом растворе), β = 0,76, для случая с 60°-ными дислокациями получаем упрощенное выражение для критической толщины:

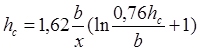(8)

1.1. 4 Движение прорастающих дислокацийв напряженных пленках

Согласно классическим представлениям [8] скорость движения дислокации может быть представлена в виде:

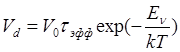(9)

где V₀ – константа, E_ν – энергия активации движения дислокации путем скольжения, τ_эфф – эффективное напряжение, действующее на дислокацию. Величина эффективного напряжения пропорциональна ε (а на начальной стадии релаксации, когда ε ≈ f , она пропорциональна разнице параметров решеток Ge и Si) и возрастает с увеличением толщины пленки h. Таким образом, с помощью этих двух параметров ε и h можно регулировать величину эффективного напряжения, определяющую скорость движения дислокации при конкретной температуре.

1.1.5 Зарождение дислокаций несоответсвия в напряженных пленках

Зарождение дислокационной петли в напряженной пленке аналогично зарождению новой фазы (например, появлению зародыша твердой фазы в переохлажденной жидкости) и требует затраты какого-то количества энергии. Энергия дислокационной петли радиуса R согласно Мэтьюзу [9] равна

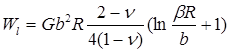(10)

Выигрыш за счет уменьшения напряжений при образовании такой петли внутри напряженной пленки равен

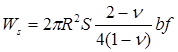(11)

Видно, что дополнительная энергия появившейся дислокационной петли пропорциональна радиусу, а уменьшение энергии напряжений при этом – квадрату радиуса дислокационной петли. Соответственно, алгебраическая сумма этих энергий в зависимости от R должна иметь максимум, как показано на рисунке 1.1. Этот максимум является тем энергетическим барьером, преодоление которого возможно при флуктуационном достижении дислокационной петлей критического радиуса R (рис. 1.1).

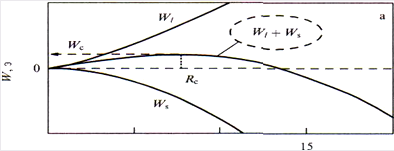
Рис. 1.1 Пример расчёта для определения критического радиуса дислокационной петли и энергии её образования для Ge_0,3 Si_0,7 /Si(001).

На рисунке 1.1 изображены зависимости W_s и W_l , а также их суммы W_s + W_l , от радиуса дислокационной петли для доли Ge в пленке, равной 0,3. Видно, что расчётный энергетический барьер образования такой петли W_c составляет около 250 эВ. Более точные расчеты с учетом типа дислокации, энергии ступени, образующейся на поверхности пленки при прохождении дислокационной полупетли через ее объем, учет различных значений параметра ядра дислокации β [10,11] дают несколько меньшие значения W_c , которые, тем не менее, близки или превышают 100 эВ для концентрации Ge ≤ 0,3 в твердом растворе GeSi. На основе таких расчетов был сделан вывод о невозможности гомогенного зарождения ДН в псевдоморфных пленках Ge_x Si_{1- x} с х до 0,5 [10]. Тем не менее ДН в таких гетероструктурах возникают.