Доклад: Эквивалентность элементарных функций

студента группы ТК

четвертого курса

Польщи М.В.

Научный руководитель: профессор Лисовик Леонид Петрович

Определение. Функция называется элементарной по Кальмару, если ее можно получить й из функций s¹ , Iⁿ _m ,x+y,x-y,S, а также конечного применения операцийсуммирования и мультиплицирования.

Определим пять классов функций, элементарных по Кальмару.

L₁ ­ Класс функций, получаемый из функций s¹ , Iⁿ _m ,x+y,x-y,S, а также конечного применения операцийсуммирования и мультиплицирования.

L ₂ ­ Класс функций, получаемый из функций s¹ , Iⁿ _m ,x-y, 2^x ,S, а также конечного применения операции суммирования.

L ₃ ­ Класс функций, получаемый из функций s¹ , Iⁿ _m ,x-y,x*y, 2^x ,S, а также конечного применения операции ограниченной минимизации.

L ₄ ­ Класс функций, получаемый из функций s¹ , Iⁿ _m ,x-y,x+y 2^x ,S, а также конечного применения операции ограниченной рекурсии.

L ₅ ­ Класс функций, получаемый из функций s¹ , Iⁿ _m ,x-y,x*y, S, а также конечного применения операции мультиплицирования.

Доказательство будем проводить по следующей схеме:

1. L ₁ L ₂ L ₃ L ₄ L ₁

2. L ₁ L ₅

3. L ₅ L ₃

Докажем, что L ₁ L ₂ (для этого выразим 2^x через функции L ₁ )

Докажем, что L ₂ L ₃ (для этого выразим x*y и операцию ограниченной минимизации через функции L ₂ )

Пусть

тогда

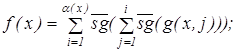
Докажем, что L₃ L₄ (для этого выразим x+y и операцию ограниченной рекурсии через функции L ₃ )

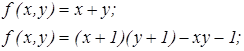
Выразим операцию ограниченной рекурсии на основании следующего свойства функции Геделя.

Пусть

тогда

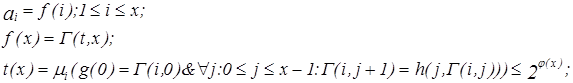
--> ЧИТАТЬ ПОЛНОСТЬЮ <--