Доклад: Объекты нечисловой природы
Статистика объектов нечисловой природы - это направление в математической статистике, в котором в качестве статистических данных (результатов наблюдений) рассматриваются объекты нечисловой природы. Так называют объекты, которые нецелесообразно описывать числами, в частности элементы нелинейных пространств. Примерами являются бинарные отношения (ранжировки, разбиения, толерантности и др.), результаты парных и множественных сравнений, множества, нечеткие множества, измерение в шкалах, отличных от абсолютных. Этот перечень примеров не претендует на законченность. Он складывался постепенно в соответствии с исследованиями в области статистики объектов нечисловой природы.
Объекты нечисловой природы широко используются в теоретических и прикладных исследованиях по проблемам управления, в частности управления качеством продукции, в технических науках, медицине, социологии, экономике, психологии и т.д., а также практически во всех отраслях народного хозяйства. Это обосновывает целесообразность дальнейшего развития рассматриваемого математико-статистического аппарата.
В журнале " Заводская лаборатория " опубликовано два обзора [1,2] и несколько десятков статей ([3-33] и др.) по различным вопросам статистики объектов нечисловой природы. Однако литературы, в которой бы разъяснялись основные понятия этого направления анализа статистических данных, явно не хватает. Данный обзор и посвящен первоначальному знакомству с основными видами объектов нечисловой природы.
Основные понятия репрезентативной теории измерений
Начнем с рассмотрения конкретного социологического исследования. Обсуждение можно вести в терминах экспертных оценок. Тогда вместо сравнения математики и физики n экспертов (а не выпускников школ) оценивают по конкурентоспособности на мировом рынке, например, две марки стали. Однако в настоящее время социологические исследования более привычны, чем экспертные.
При изучении привлекательности различных профессий для выпускников новосибирских школ [34] был составлен список из 30 профессий. Опрашиваемых просили оценить каждую из этих профессий одним из баллов 1,2,...,10 по правилу: чем больше нравится, тем выше балл. Для получения социологических выводов необходимо было дать единую оценку привлекательности определенной профессии для совокупности выпускников школ. В качестве такой оценки в работе [34] использовалось среднее арифметическое баллов, выставленных профессии опрошенными школьниками. В частности, физика получила средний балл 7.69, а математика - 7.50. В соответствии с логикой [34], физика более предпочтительна, чем математика.
Однако было отмечено [35], что этот вывод противоречит данным работы [36], согласно которым ленинградские школьники средних классов больше любят математику, чем физику. Обсудим одно из возможных объяснений этого противоречия, которое заключается в неадекватной методике обработки данных, применных в работе [34].
Дело в том, что баллы 1,2,...,10 введены исследователем-социологом, т.е. субъективно. Если одна профессия оценена в 10 баллов, а вторая - в 2, то из этого нельзя заключить, что первая ровно в 5 раз привлекательней другой. Другой коллектив социологов мог бы принять иную систему баллов, например 1,4,9,16,...,100. Естественно предположить , что упорядочивание профессий по привлекательности, присущее школьникам, не зависит от того, какой системой баллов им предложит пользоваться социолог. Раз так, то распределение профессий по градациям десятибалльной системы не изменится, если перейти к другой системе баллов с помощью строго возрастающей функции ![]() .Если
.Если ![]() -ответы n выпускников школ, касающихся математики, а
-ответы n выпускников школ, касающихся математики, а ![]() -физики, то после перехода к новой системе баллов ответы относительно математики будут иметь вид
-физики, то после перехода к новой системе баллов ответы относительно математики будут иметь вид ![]() ,а относительно физики -
,а относительно физики - ![]() .
.
Пусть единая оценка привлекательности профессии вычисляется с помощью функции. ![]() . Какие требования естественно наложить на функцию
. Какие требования естественно наложить на функцию ![]() , чтобы полученные с ее помощью выводы не зависели от того, какой именно системой баллов пользовался социолог ?
, чтобы полученные с ее помощью выводы не зависели от того, какой именно системой баллов пользовался социолог ?
Единая оценка вычислялась для того, чтобы сравнивать профессии по привлекательности. Поэтому потребуем устойчивости результата сравнения: неравенство
(1)
справедливо тогда и только тогда, когда справедливо неравенство
 , (2)
, (2)
причем равносильность неравенств (1) и (2) имеется при любых ![]() и
и ![]() . Какие
. Какие ![]() устойчивы относительно сравнения? Ответ на этот вопрос был дан в работе [35]. В частности, оказалось, что средним арифметическим, как в работе [34], пользоваться нельзя, а членами вариационного ряда (и только ими) - можно.
устойчивы относительно сравнения? Ответ на этот вопрос был дан в работе [35]. В частности, оказалось, что средним арифметическим, как в работе [34], пользоваться нельзя, а членами вариационного ряда (и только ими) - можно.
Выше показан переход от социологической задачи к математической (подробнее см. [37, § 3.1], [38]), а именно, к одной из частных постановок проблемы адекватности в репрезентативной теории измерения [39, 40]. Изложим основные понятия этой теории в модификации , данной в работе [ 37 гл. 3 ].
Исходным понятием является совокупность Ф={![]() }. допустимых преобразований шкалы (обычно Ф- группа),
}. допустимых преобразований шкалы (обычно Ф- группа),![]() . Алгоритм обработки данных а , т.е. функция
. Алгоритм обработки данных а , т.е. функция ![]() .(А - множество возможных результатов работы алгоритма) называется в шкале совокупностью допустимых преобразований Ф адекватным [ 37, c. 97], если
.(А - множество возможных результатов работы алгоритма) называется в шкале совокупностью допустимых преобразований Ф адекватным [ 37, c. 97], если
![]() (3)
(3)
для всех ![]() , i=1,...,n и всех
, i=1,...,n и всех ![]() Ф. Таким образом, теорию измерений рассматриваем как теорию инвариантов относительно различных совокупностей допустимых преобразований Ф. Интерес вызывают две задачи: а) дано Ф; какие а из определенного класса удовлетворяют условию (3); б) дан алгоритм а ; для каких Ф справедливо условие (3)? Уточнение этих постановок дано в работах [ 37, 41, 42 ]
Ф. Таким образом, теорию измерений рассматриваем как теорию инвариантов относительно различных совокупностей допустимых преобразований Ф. Интерес вызывают две задачи: а) дано Ф; какие а из определенного класса удовлетворяют условию (3); б) дан алгоритм а ; для каких Ф справедливо условие (3)? Уточнение этих постановок дано в работах [ 37, 41, 42 ]
Наиболее распространенные шкалы измерения описываются с помощью групп допустимых преобразований Ф. Если Ф состоит из всех взаимнооднозначных преобразований , то измерения проводятся в шкале наименований. Для порядковой шкалы Ф состоит из всех строго возрастающих преобразований. по этим двум шкалам измеряются качественные признаки.
Для шкалы интервалов Ф={ах+b; а>0,![]() }, для шкалы отношений Ф=ах;а>0}, для шкалы разностей Ф={х+b;
}, для шкалы отношений Ф=ах;а>0}, для шкалы разностей Ф={х+b;![]() },для абсолютной шкалы Ф={
},для абсолютной шкалы Ф={![]() , По этим четырем шкалам измеряются количественные признаки. В абсолютной шкале известно начало отсчета и единица измерения, в шкале отношений фиксированно начало , но не единица измерения, в шкале разностей, наоборот, единица измерения фиксирована, а начало отсчета - нет , в шкале интервалов ни то, ни другое не задано.
, По этим четырем шкалам измеряются количественные признаки. В абсолютной шкале известно начало отсчета и единица измерения, в шкале отношений фиксированно начало , но не единица измерения, в шкале разностей, наоборот, единица измерения фиксирована, а начало отсчета - нет , в шкале интервалов ни то, ни другое не задано.
Различные свойства шкал, примеры реальных величин, измеряемых по тем или иным шкалам, приведены в работах [37, 39, 40,43].
Бинарные отношения.
Пусть а :![]() - адекватный алгоритм в шкале наименований. Легко видеть [37,c.109] , что a - есть функция от матрицы B =
- адекватный алгоритм в шкале наименований. Легко видеть [37,c.109] , что a - есть функция от матрицы B =![]() =В (
=В (![]() ), где
), где
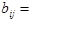
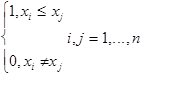 .
.
Если a :![]() - адекватный алгоритм в шкале порядка, то a есть [37,c.111] функция от матрицы C =
- адекватный алгоритм в шкале порядка, то a есть [37,c.111] функция от матрицы C =![]() =C (
=C (![]() ) порядка n x n, где
) порядка n x n, где
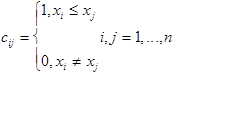
Матрицы B и C можно проинтерпретировать в терминах бинарных отношений. Пусть некоторая характеристика измеряется у n объектов ![]() , причем
, причем ![]() - результат ее измерения у объекта
- результат ее измерения у объекта ![]() Тогда матрицы B и C задают бинарные отношения на множестве объектов Q ={
Тогда матрицы B и C задают бинарные отношения на множестве объектов Q ={![]() }Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата Q x Q, то любой матрице D =
}Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата Q x Q, то любой матрице D = ![]() порядка n x n из 0 и 1 соответствует бинарное соотношение R(D ), определяемое следующим образом:
порядка n x n из 0 и 1 соответствует бинарное соотношение R(D ), определяемое следующим образом: ![]() R(D ) тогда и только тогда, когда
R(D ) тогда и только тогда, когда ![]() 1.
1.
Бинарное отношение R(B ) - отношение эквивалентности, т.е. рефлексивное симметричное транзитивное отношение. Оно задает разбиение Q на классы эквивалентности. Два объекта ![]() и
и ![]() входят в один класс эквивалентности тогда и только тогда, когда
входят в один класс эквивалентности тогда и только тогда, когда ![]() .
.
Выше показано, как разбиения возникают в результате измерений в шкале наименований. Разбиения могут появляться и непосредственно. Так, при оценке качества промышленной продукции эксперты дают разбиение показателей качества на группы [44]. Для изучения психологического состояния людей их просят разбить предъявленные рисунки на группы сходных между собой [45,46].Аналогичная методика применяется в экспериментальных психологических исследованиях. [47,48].
Во многих задачах прикладной статистики разбиения получаются "на выходе" (в кластер-анализе) или же используются на промежуточных этапах анализа данных (например, сначала проводят классификацию с целью выделения однородных групп, а затем в каждой группе строят регрессионную зависимость, как в работе [49]).
Бинарное отношение R(С ) задает разбиение Q на классы эквивалентности, между которыми введено отношение строгого порядка. Два объекта ![]() и
и ![]() входят в один класс тогда и только тогда, когда
входят в один класс тогда и только тогда, когда ![]() = 1 и
= 1 и ![]() = 1, т.е.
= 1, т.е. ![]() Класс эквивалентности
Класс эквивалентности ![]() предшествует классу эквивалентности
предшествует классу эквивалентности ![]() тогда и только тогда, когда для любых
тогда и только тогда, когда для любых ![]()
![]() ,
, ![]()
![]() имеем ,
имеем , ![]() = 1,
= 1,![]() = 0, т.е.
= 0, т.е.![]() . Такое бинарное отношение в статистике называют ранжировкой со связями [50]; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок [51], упорядочение [52,гл.2], квазисерия [53, с.37]. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).
. Такое бинарное отношение в статистике называют ранжировкой со связями [50]; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок [51], упорядочение [52,гл.2], квазисерия [53, с.37]. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).
Как известно, ранжировки возникают в результате измерений в порядковой шкале. Так, при описанном выше опросе ответ выпускника школы - это ранжировка (со связями) профессий по привлекательности. Ранжировки часто возникают и непосредственно, без промежуточного этапа - приписывания объектам квазичисловых оценок - баллов. Многочисленные примеры тому даны М.Кендэлом [50]. При оценке качества промышленной продукции нормативные методические документы предусматривают использование ранжировок [44].
--> ЧИТАТЬ ПОЛНОСТЬЮ <--