Математика / Книга: Множественная регрессия и корреляция 2

Книга: Множественная регрессия и корреляция 2

3. Провести две независимых регрессии первых наблюдений и последних наблюдений и найти, соответственно, и . Из и выбираем большую и меньшую величины, соответственно, и .

4. Составить статистику и найти по распределению Фишера , где – число объясняющих переменных модели.

5. Если , то гипотеза отвергается, т.е. модель гетероскедастична, а если , то гипотеза принимается, т.е. модель гомоскедастична.

Тест Бреуша – Пагана (Breusch - Pagan)

Этот тест применяется в тех случаях, когда предполагается, что дисперсии зависят от некоторых дополнительных переменных. Пусть , . Тест состоит в следующем:

1. Провести обычную регрессию и получить . (Для этого в диалоговом окне Регрессия установить флажок на функцию Остатки )

2. Построить оценку .

3. Провести регрессию и найти для нее объясненную часть вариации .

4. Построить статистику .

5. Если (где p – число переменных, от которых зависит ), то имеет место гетероскедастичность.

Если , то - гомоскедастичность.

- критическая точка распределения (хи-квадрат) при выбранном уровне значимости , для нахождения которой выполнить следующую последовательность действий: fx Статистические ХИ2ОБР

Тест Дарбина – Уотсона (Darbin-Watson) на наличие автокорреляции

Этот тест используется для обнаружения автокорреляции первого порядка, т.е. проверяется некоррелированность не любых, а только соседних величин . Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной значения .

Гипотеза (автокорреляция отсутствует).

Общая схема критерия Дарбина – Уотсона следующая:

1. По эмпирическим данным построить уравнение регрессии по МНК и определить значения отклонений для каждого наблюдения t (t = 1, 2, …, n).

2. Рассчитать статистику DW :

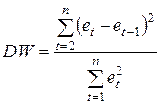
3. По таблице критических точек распределения Дарбина –Уотсона для заданного уровня значимости , числа наблюдений и количества объясняющих переменных определить два значения: - нижняя граница и - верхняя граница (таблица 2).

Полный вариант таблицы приведен в разделе Математико-статистические таблицы (Таблица 5. Значения dH и dB критерия Дарбина—Уотсона на уровне значимости  = 0,05 (n — число наблюдений, р — число объясняющих переменных). множественный корреляция регрессия

Таблица 2.

Статистика Дарбина – Уотсона, уровень значимости 0,05
	1		2		3		4		5

20	1,20	1,41	1,1	1,54	1,00	1,67	0,90	1,83	0,79	1,99
21	1,22	1,42	1,13	1,54	1,03	1,66	0,93	1,81	0,83	1,96
22	1,24	1,43	1,15	1,54	1,05	1,66	0,96	1,80	0,86	1,94
23	1,26	1,44	1,17	1,54	1,08	1,66	0,99	1,79	0,90	1,92
24	1,27	1,45	1,19	1,55	1,10	1,66	1,01	1,78	0,93	1,90
25	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89