Книга: Одномерные массивы

2.9 Поиск минимального и максимального элемента массива и его порядкового номера (индекса)

Пусть требуется найти минимальный элемент (min ) и его индекс (n_min ) во всем массиве (in=0 и ik=n ) или какой то его части (с in – го по ik – ый), в этом случаи алгоритм решения задачи можно записать так:

1. в качестве начального значения переменной min выберем любой из рассматриваемых элементов (обычно выбирают первый). Тогда min=a_in , n_min= in;

2. затем в цикле по параметру i начиная со следующего элемента (i=in+1, …, ik ) будем сравнивать элементы массива a_i текущим минимальным min . Если окажется, что текущий (i – ый ) элемент массива меньше минимального (a_i < min ), то переменная min принимает значение a_i , а n_min – на i : min =a_i , n_min = i .

Графическая схема алгоритма и фрагмент программы поиска минимального элемента в массиве приведены на рисунке 2.16.

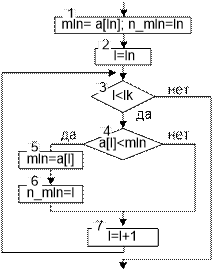min=a[in]; n_min=in; for(i=in+1; i<ik; i++) if(a[i]<min) { min=a[i]; n_min=i; }

Рисунок 2.16. Графический алгоритм и фрагмент программы поиска минимального элемента в массиве

Заметим, что при наличии в массиве нескольких минимальных элементов, найден будет первый из них (самый левый минимальный элемент) при просмотре массива слева направо. Если в неравенстве a_i < min знак > поменять на знак ≥ , то будет найден последний из них (самый правый минимальный элемент).

Для поиска максимального элемента max и его индекса n_max используется аналогичный алгоритм, в котором сначала надо принять max =a_in , n_ max = in , вместо неравенства a_i < min используется неравенство a_i > max . В случаи выполнения условия a_i > max записать в max =a_i и в n_ max = i .

Для поиска в массиве экстремума можно не использовать вспомогательную переменную min (max ). В этом случаи минимальный элемент массива определяется только по его индексу n_min (n_max ) (рисунок 2.17).

« 6 7 8 9 10 11 12 13 14 15 » К-во Просмотров: 1175 Бесплатно скачать Книга: Одномерные массивы >>> Скачать <<< Меню Поиск