Книга: Прикладная теория информации
Контрольные вопросы
1. В чем сущность принципиальных различий в трактовке понятия информации?
2. Каковы основные этапы обращения информации?
3. Охарактеризуйте разновидности информационных систем и тенденции их развития.
4. Совокупность, каких объектов составляет систему передачи информации?
5. Что понимают под сообщением и сигналом?
6. В чем различие между линией и каналом связи?
7. Объясните разницу в уровнях проблем передачи информации.
8. Каковы основные задачи теории информации?
9. В чем сущность теоретико-информационного подхода к исследованиям?
Глава 1. Математические модели сигналов
§ 1.1 Понятия сигнала и его модели
Как указывалось во введении, понятие "сигнал" имеет неоднозначное толкование. В широком смысле слова под сигналом понимают материальный носитель информации. При этом к сигналам относят как естественные сигналы, так и сигналы, специально создаваемые с определенной целью. Естественными являются, например, световые сигналы, позволяющие видеть окружающий мир, космические сигналы. Примером специально создаваемых могут служить сигналы, генерируемые с целью извлечения информации об изменениях в объекте или процессе (эталонные сигналы).
В дальнейшем понятие "сигнал", если это не оговорено специально, будет использоваться в узком смысле как сигнал, специально создаваемый для передачи сообщения в информационной системе. Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем (переносчиком) информации (сообщения). Носитель становится сигналом в процессе модуляции. Параметры носителя, изменяемые во времени в соответствии с передаваемым сообщением, называют информативными.
В качестве носителей информации используются колебания различной природы, чаще всего гармонические, включая частный случай - постоянное состояние (ω = 0). В технических информационных системах наиболее широкое распространение получили носители в виде электрического напряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности, будем соотносить их с электрическими сигналами.
В носителе u(t) = const имеется только один информативный параметр - уровень (например, уровень напряжения). При использовании гармонических электрических колебаний информативными могут стать такие параметры, как амплитуда, частота, фаза. Колебания принято подразделять на детерминированные и случайные.
Детерминированными называют колебания, которые точно определены в любые моменты времени.
Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.
При изучении общих свойств каналов связи, сигналов и помех мы отвлекаемся от их конкретной физической природы, содержания и назначения, заменяя моделями. Модель - это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.
Задачи повышения эффективности функционирования информационных систем связаны с установлением количественных соотношений между основными параметрами, характеризующими источник информации и канал связи. Поэтому при исследовании используют математические модели. Математическое моделирование может быть реализовано различными методами в зависимости от способа, которым определяются интересующие нас показатели.
Фундаментальные исследования базируются на методе аналитического моделирования, заключающемся в создании совокупности математических соотношений, позволяющих выявить зависимости между параметрами модели в общем виде. При этом широко используются модели, параметры которых противоречат физическим свойствам реальных объектов. Например, модель сигнала часто представляется суммой бесконечного числа функций, имеющих неограниченную продолжительность (синусоид). Поэтому важно обращать внимание на условия, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.
Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать точно изменения значения информативного параметра невозможно. Следовательно, сигнал принципиально представляет собой случайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.
Тем не менее, в случае детерминированного колебания условно так же говорят о детерминированном сигнале. Такой сигнал отображает известное сообщение, которое нет смысла передавать. Ему соответствует модель в виде функции, полностью определенной во времени.
Изучение моделей детерминированных сигналов необходимо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются основой для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный процесс. Детерминированное колебание, таким образом, представляет собой вырожденную форму случайного процесса со значениями параметров, известными в любой момент времени с вероятностью, равной единице. Детерминированные сигналы имеют и самостоятельное значение. Они специально создаются для целей измерения, наладки и регулирования объектов информационной техники, выполняя роль эталонов.
§ 1.2 Формы представления детерминированных сигналов
В зависимости от структуры информационных параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.
Сигнал считают дискретным по данному параметру, если число значений, которое может принимать этот параметр, конечно (или счетно). Если множество возможных значений параметра образует континуум, то сигнал считают непрерывным по данному параметру. Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-
 |
???????????.
В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:
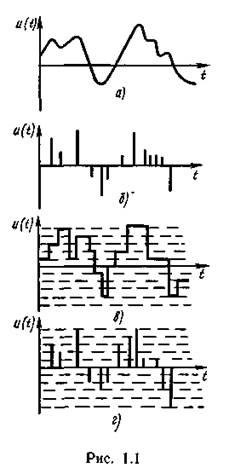
непрерывная функция непрерывного аргумента, например непрерывная функция времени (рис.1.1, а);
непрерывная функция дискретного аргумента, например функция, значения которой отсчитывают только в определенные моменты времени (рис.1.1, б);
дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис.1.1, в);
дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис.1.1, г).