Книга: Проектирование судов Теория проектирования
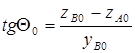 .
.
При изменении масштаба по оси y в b раз, а по оси z в t раз, точки А 0 и В 0 перейдут в точки А и В , с координатами А (0; tzА 0 ) и В (byВ 0 ; tzВ 0 ). Тогда,
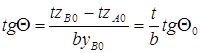 .
.
Аналогично можно найти, как соотносятся длины отрезков прототипа и проекта. Пусть а 0 = А 0 В 0 – длина какого-то отрезка прототипа, расположенного под углом Θ0 к оси у (см. рис. 2). Проекция отрезка на эту ось,
А 0 С 0 = а 0 Соs Q0 .
При изменении масштаба вдоль оси у в b раз отрезок трансформируется в а' = А'В' , расположенный под углом Θ' . При этом его проекция на ось у ,
А'С' = b (А 0 С 0 ) = b а 0 Соs Q0 .
Изменение масштаба по оси z в t раз переместит точки А' , В' и С' , соответственно в А , В и С . Отрезок а = АВ , расположенный под углом Θ к оси у будет связан с а 0 следующими соотношениями:
АС = А'С' = b (А 0 С 0 ) = b а 0 Соs Q0 ,
Откуда
![]() .
.
При Q = 0 данное выражение совпадает с полученными ранее выражениями для L , В и T . Поперечный момент инерции проектируемого судна при Q ¹ 0 с учетом выражения полученного ранее для Ix .
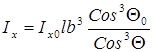 ,
,
а метацентрический радиус,
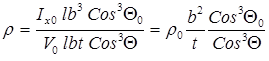 .
.
Для больших углов крена показателем остойчивости служит не метацентрическая высота, а плечо статической остойчивости lcт . Получим выражение для его определения. Из рис. 3 видно, что,
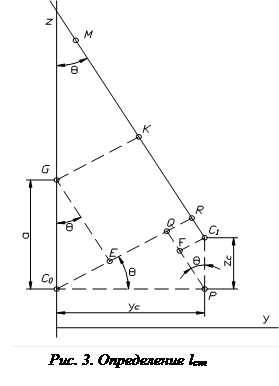
![]() .
.
Из треугольника C 0 QP ,
![]() .
.
QR = FC 1 . Из треугольника C 1 FP ,
![]() .
.
Из треугольника C 0 GE ,
![]() .
.
Окончательно получим,
lст = уСos Θ + zc Sin Θ – aSin Θ.
С учетом масштабов длин, данное выражение можно переписать в виде,
lст = bуc 0 Сos Θ + tzc 0 Sin Θ – ta 0 Sin Θ.
Частными случаями полученной зависимости будут выражения: