Книга: Устойчивость дисперсных систем седиментация и диффузия

Если , F _сед > 0 – происходит оседание частиц. Если F _сед < 0 – то частицы всплывают. Результирующая сила, действующая на частицу:

,

где B – коэффициент трения; U – скорость седиментации.

при равновесии Fсед = Fтр

???? ??????, ???????? ?????? ??????

для сферических частиц

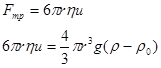
Отсюда уравнение скорости оседания и радиуса частиц

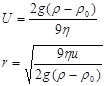
Результатами седиментационного анализа может служить интервал радиусов частиц в данной системе, просто радиус частиц или доля фракций определенного радиуса.

Способность к седиментации принято выражать через константу седиментации S , которая определяется скоростью седиментации:

Для сферических частиц эта константа равна

Из уравнения следует, что S зависит как от размеров частиц, так и от природы среды. За единицу измерения S принят сведберг (сб), равный 10¹³ с.

Часто для характеристики процесса седиментации используют удельный поток седиментации I _сед.

Удельный поток седиментации – это число частиц, оседающих в единицу времени через сечение единичной площади, нормальное к направлению седиментации.

Размерность: [i _сед ] = част/см² * с.

Из определения i _сед следует: i _сед = U_сед * v , где v – частичная концентрация частиц в дисперсной системе.

Подставив в это уравнение U _сед , получим:

Таким образом, удельный поток прямо пропорционален V , v , (ρ – ρ_о ) и обратно пропорционален S . Подставив эти выражения в уравнение, получим

Значит, в случае сферических частиц удельный поток прямо пропорционален квадрату радиуса и обратно пропорционален вязкости среды.

Рассматривая процесс седиментации, мы не учитываем броуновского движения, в котором участвуют частицы. Следствием броуновского движения, является диффузия, которая стремится выровнять концентрацию частиц по всему объёму, в то время как седиментация приводит к увеличению концентрации в нижних слоях.

Таким образом, наблюдается два противоположных потока: поток седиментации i _сед и поток диффузии i _диф.

, где

В результате конкуренции этих потоков возможны три варианта:

1. , т.е., т.е.

Чтобы выполнилось это неравенство, значения Т и должны быть малы, а (ρ – ρ_о ) и v – велики. В реальных условиях эти параметры заметно изменить сложно, а радиус частиц в дисперсных системах изменяется в широком интервале: от 10^-7 до 10^-2 см и именно радиус частиц является определяющим. Установлено, что данное неравенство соблюдается, когда r 10^-3 см. В этих случаях диффузией можно пренебречь, идёт быстрая седиментация – система является седиментационно неустойчивой.

2. , т.е. ,